Mathématiques > Algèbre > Équations et Inéquations > Résolution graphique d'équations et d'inéquations

Exemples de résolution graphique d'inéquations : Cas concrets

Découvrez des exemples concrets de résolution graphique d'inéquations, illustrant les différentes situations rencontrées et les techniques à appliquer.

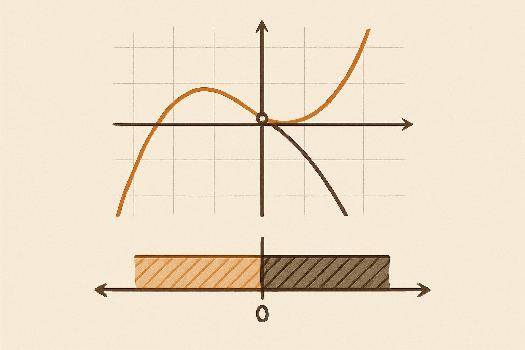
Exemple 1 : Inéquation linéaire

Résolvons graphiquement l'inéquation 2x + 1 < 5.

  1. Transformer l'inéquation : On peut réécrire l'inéquation sous la forme 2x < 4, puis x < 2.
  2. Tracer la droite : On trace la droite d'équation y = 2x + 1.
  3. Identifier la zone de solutions : On cherche les valeurs de x pour lesquelles la droite est en dessous de la droite horizontale y = 5. Cela correspond à x < 2.

Conclusion : La solution de l'inéquation est x ∈ ]-∞, 2[.

Exemple 2 : Inéquation polynomiale du second degré

Résolvons graphiquement l'inéquation x² - x - 2 > 0.

  1. Tracer la parabole : On trace la parabole d'équation y = x² - x - 2.
  2. Identifier les zéros : On trouve les points où la parabole coupe l'axe des abscisses en résolvant l'équation x² - x - 2 = 0. Les solutions sont x = -1 et x = 2.
  3. Identifier la zone de solutions : On cherche les valeurs de x pour lesquelles la parabole est au-dessus de l'axe des abscisses. Cela correspond à x < -1 et x > 2.

Conclusion : La solution de l'inéquation est x ∈ ]-∞, -1[ ∪ ]2, +∞[.

Exemple 3 : Inéquation avec une fonction rationnelle

Résolvons graphiquement l'inéquation (x + 1) / (x - 2) ≥ 0.

  1. Identifier les valeurs interdites : La fonction n'est pas définie pour x = 2.
  2. Tracer la courbe : On trace la courbe de la fonction y = (x + 1) / (x - 2).
  3. Identifier les zéros : La fonction s'annule pour x = -1.
  4. Identifier la zone de solutions : On cherche les valeurs de x pour lesquelles la courbe est au-dessus de l'axe des abscisses ou touche l'axe des abscisses (car l'inéquation est large). Cela correspond à x ≤ -1 et x > 2.

Conclusion : La solution de l'inéquation est x ∈ ]-∞, -1] ∪ ]2, +∞[.

Tableau de signe associé:

x -∞ -1 2 +∞
x + 1 - 0 + +
x - 2 - - || +
(x+1)/(x-2) + 0 || +

Exemple 4 : Inéquation avec des valeurs absolues

Résolvons graphiquement l'inéquation |x - 1| < 2.

  1. Interprétation géométrique : L'expression |x - 1| représente la distance entre x et 1 sur la droite réelle.
  2. Tracer les courbes : On trace la courbe de y = |x - 1| et la droite horizontale y = 2.
  3. Identifier la zone de solutions : On cherche les valeurs de x pour lesquelles la courbe de la valeur absolue est en dessous de la droite y = 2. Cela correspond à -1 < x < 3.

Conclusion : La solution de l'inéquation est x ∈ ]-1, 3[.

Ce qu'il faut retenir

  • La résolution graphique d'inéquations nécessite de tracer les courbes des fonctions impliquées.
  • Les solutions sont les intervalles des abscisses où la courbe satisfait l'inégalité.
  • Il est important de prendre en compte les valeurs interdites (si la fonction n'est pas définie pour certaines valeurs).
  • La méthode graphique peut être combinée avec un tableau de signes pour une analyse plus rigoureuse.

← Comprendre les Suites Numériques : Explicites et Récurrentes Exercices : Opérations sur les Fonctions →

FAQ

  • Comment choisir l'échelle du graphique ?

    L'échelle du graphique doit être choisie de manière à visualiser clairement les points d'intersection et les zones où la courbe est au-dessus ou en dessous des autres courbes. Il est souvent nécessaire d'ajuster l'échelle pour obtenir une lecture précise des solutions.
  • Que faire si l'inéquation est complexe ?

    Si l'inéquation est complexe, il peut être utile de la simplifier algébriquement avant de la résoudre graphiquement. On peut également utiliser un logiciel de traçage de courbes pour faciliter la construction du graphique.