Chemins et Cycles dans les Graphes : Exploration et Applications

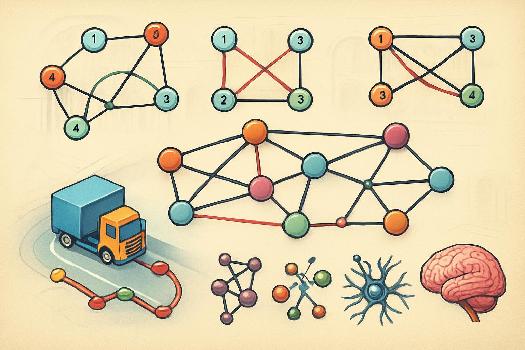
Définitions de base : Chemins et Cycles

Un chemin dans un graphe est une séquence de sommets reliés par des arêtes. La longueur d'un chemin est le nombre d'arêtes qu'il contient.

Un cycle est un chemin qui commence et se termine au même sommet. En d'autres termes, c'est un chemin fermé.

Par exemple, dans un graphe où A est relié à B, B à C et C à A, le chemin A-B-C-A est un cycle. Le chemin A-B-C est un simple chemin.

Il existe différents types de chemins et de cycles, notamment les chemins et cycles simples (où aucun sommet n'est répété, sauf le point de départ et d'arrivée pour un cycle) et les chemins et cycles élémentaires (où aucune arête n'est répétée). Un chemin simple est toujours élémentaire, mais l'inverse n'est pas toujours vrai.

Chemins Eulériens et Cycles Eulériens

Un chemin eulérien est un chemin qui emprunte chaque arête du graphe exactement une fois. Un cycle eulérien est un chemin eulérien qui commence et se termine au même sommet.

Théorème d'Euler : Un graphe connexe admet un cycle eulérien si et seulement si tous ses sommets ont un degré pair (c'est-à-dire, un nombre pair d'arêtes incidentes). Un graphe connexe admet un chemin eulérien (mais pas un cycle) si et seulement si exactement deux de ses sommets ont un degré impair.

Exemple : Imaginez un plan de ville où vous voulez traverser chaque rue exactement une fois. L'existence d'un chemin ou d'un cycle eulérien vous dit si c'est possible. Si plus de deux intersections ont un nombre impair de rues qui s'y croisent, ce n'est pas possible.

Algorithme de Hierholzer (pour trouver un cycle eulérien) :

1. Choisir un sommet de départ (n'importe lequel si tous les sommets ont un degré pair).
2. Parcourir le graphe en suivant les arêtes de manière arbitraire, en veillant à ne pas réutiliser la même arête. À chaque sommet visité, supprimer l'arête utilisée.
3. Si vous revenez au sommet de départ avant d'avoir utilisé toutes les arêtes, vous avez trouvé un cycle partiel.
4. Choisir un sommet sur ce cycle partiel qui a encore des arêtes non utilisées.
5. Recommencer l'étape 2 à partir de ce sommet jusqu'à revenir au sommet de départ (créant un autre cycle partiel).
6. Combiner les cycles partiels pour former le cycle eulérien complet.

Chemins Hamiltoniens et Cycles Hamiltoniens

Un chemin hamiltonien est un chemin qui visite chaque sommet du graphe exactement une fois. Un cycle hamiltonien est un chemin hamiltonien qui commence et se termine au même sommet.

Contrairement aux chemins eulériens, il n'existe pas de condition nécessaire et suffisante simple pour l'existence d'un chemin ou d'un cycle hamiltonien. C'est un problème beaucoup plus difficile à résoudre en général (NP-complet).

Quelques conditions suffisantes (mais non nécessaires) :

• Théorème de Dirac : Si un graphe simple de n sommets (avec n ≥ 3) est tel que chaque sommet a un degré d'au moins n/2, alors il contient un cycle hamiltonien.
• Théorème d'Ore : Si un graphe simple de n sommets (avec n ≥ 3) est tel que la somme des degrés de deux sommets non adjacents quelconques est au moins n, alors il contient un cycle hamiltonien.

Algorithmes de recherche : Étant donné la difficulté du problème, les algorithmes de recherche de chemins hamiltoniens sont souvent basés sur des approches heuristiques (qui ne garantissent pas de trouver une solution, mais qui sont efficaces dans la pratique) ou des recherches exhaustives (qui testent toutes les possibilités, mais qui peuvent être très coûteuses en temps de calcul pour les grands graphes). L'algorithme le plus simple est la recherche en profondeur (Depth-First Search, DFS) avec backtracking.

Exemple : Le problème du voyageur de commerce (TSP) est une application classique des cycles hamiltoniens. Le but est de trouver le cycle hamiltonien de coût minimal (où le coût d'une arête représente la distance entre deux villes, par exemple).

Applications

Les chemins et cycles dans les graphes ont de nombreuses applications dans divers domaines :

• Logistique et transport : Optimisation des itinéraires de livraison, planification de tournées.
• Réseaux informatiques : Routage des données, conception de réseaux.
• Biologie : Analyse des réseaux d'interaction protéique, modélisation des voies métaboliques.
• Chimie : Représentation des molécules et des réactions chimiques.
• Intelligence artificielle : Recherche de solutions dans les jeux et les problèmes d'optimisation.

Ce qu'il faut retenir

• Chemin : Séquence de sommets reliés par des arêtes.
• Cycle : Chemin qui commence et se termine au même sommet.
• Chemin eulérien : Emprunte chaque arête une fois. Un cycle eulérien existe si tous les sommets ont un degré pair.
• Chemin hamiltonien : Visite chaque sommet une fois. Problème NP-complet, algorithmes heuristiques.
• Applications : Logistique, réseaux, biologie, chimie, IA.
• L'algorithme de Hierholzer permet de trouver un cycle eulérien.
• Les théorèmes de Dirac et d'Ore donnent des conditions suffisantes pour l'existence de cycles hamiltoniens.