Mathématiques > Analyse > Intégration > Calcul de volumes (notions)

Calcul de Volumes avec Intégrales Multiples

Un guide pour comprendre et maîtriser le calcul de volumes avec les intégrales doubles et triples, avec des exemples et explications adaptées au niveau lycée.

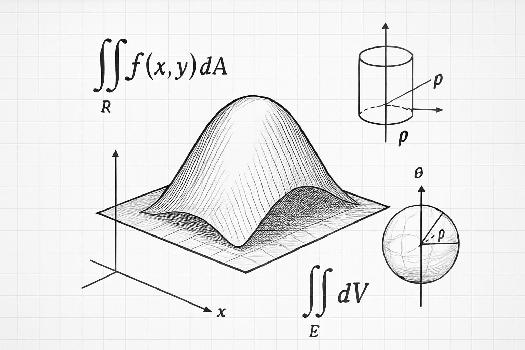
Introduction aux Intégrales Doubles et Triples pour le Calcul de Volumes

Les intégrales doubles et triples sont des outils puissants pour calculer les volumes de régions complexes dans l'espace. Alors que l'intégrale simple permet de calculer l'aire sous une courbe, les intégrales doubles et triples permettent de calculer le volume sous une surface et dans une région 3D respectivement. L'idée de base est de diviser la région en petits éléments de volume, d'approximer le volume de chaque élément, puis de sommer ces volumes en utilisant une intégrale multiple.

Intégrales Doubles et Volumes

Une intégrale double permet de calculer le volume d'un solide situé sous une surface z = f(x, y) et au-dessus d'une région R dans le plan xy.

Étapes :

  1. Définissez la région d'intégration R dans le plan xy. Cette région peut être définie par des inégalités telles que a ≤ x ≤ b et g(x) ≤ y ≤ h(x).
  2. Définissez la fonction z = f(x, y) qui représente la surface supérieure du solide.
  3. Calculez l'intégrale double : V = ∬R f(x, y) dA, où dA est l'élément d'aire (dx dy ou dy dx).

Exemple : Trouvez le volume du solide borné par le plan z = 4 - x - y et les plans x = 0, y = 0, et z = 0.
Solution: La région R dans le plan xy est un triangle borné par x = 0, y = 0 et x + y = 4. Donc, 0 ≤ x ≤ 4 et 0 ≤ y ≤ 4 - x.
V = ∫[0, 4] ∫[0, 4-x] (4 - x - y) dy dx = ∫[0, 4] [4y - xy - y²/2] de 0 à (4-x) dx = ∫[0, 4] (4(4-x) - x(4-x) - (4-x)²/2) dx = 16/3 unités cubiques.

Intégrales Triples et Volumes

Une intégrale triple permet de calculer le volume d'une région 3D directement. Imaginez une région E dans l'espace. Le volume de E est donné par l'intégrale triple de la fonction constante 1 sur la région E.

Étapes :

  1. Définissez la région d'intégration E dans l'espace. Cette région peut être définie par des inégalités telles que a ≤ x ≤ b, g(x) ≤ y ≤ h(x), et u(x, y) ≤ z ≤ v(x, y).
  2. Calculez l'intégrale triple : V = ∭E dV, où dV est l'élément de volume (dx dy dz, dy dx dz, etc.).

Exemple : Trouvez le volume du tétraèdre borné par les plans x = 0, y = 0, z = 0, et x + y + z = 1.
Solution: La région E est définie par 0 ≤ x ≤ 1, 0 ≤ y ≤ 1 - x, et 0 ≤ z ≤ 1 - x - y.
V = ∫[0, 1] ∫[0, 1-x] ∫[0, 1-x-y] dz dy dx = ∫[0, 1] ∫[0, 1-x] (1 - x - y) dy dx = ∫[0, 1] [(1 - x)y - y²/2] de 0 à (1-x) dx = ∫[0, 1] ((1 - x)² - (1 - x)²/2) dx = ∫[0, 1] (1 - x)²/2 dx = [-((1 - x)³/6)] de 0 à 1 = 1/6 unités cubiques.

Coordoonées Cylindriques et Sphériques

Dans certains cas, l'utilisation des coordonnées cylindriques ou sphériques peut simplifier le calcul des intégrales multiples.

Coordonnées Cylindriques: Utiles pour les régions ayant une symétrie cylindrique. Transformations : x = r cos(θ), y = r sin(θ), z = z. dV = r dz dr dθ.
Coordonnées Sphériques: Utiles pour les régions ayant une symétrie sphérique. Transformations : x = ρ sin(φ) cos(θ), y = ρ sin(φ) sin(θ), z = ρ cos(φ). dV = ρ² sin(φ) dρ dφ dθ.

Ce qu'il faut retenir

  • Intégrales Doubles: Calcul du volume sous une surface z = f(x, y) : V = ∬R f(x, y) dA.
  • Intégrales Triples: Calcul direct du volume d'une région 3D : V = ∭E dV.
  • Le choix de l'ordre d'intégration (dx dy, dy dx, etc.) peut affecter la difficulté du calcul.
  • Les coordonnées cylindriques et sphériques peuvent simplifier les intégrales pour les régions ayant une symétrie particulière.

← Calcul d'aires sous une courbe : Introduction à l'intégration Calcul de Volumes par Intégration →

FAQ

  • Comment choisir l'ordre d'intégration dans une intégrale double?

    Choisissez l'ordre d'intégration qui simplifie le calcul. Essayez les deux ordres (dx dy et dy dx) et choisissez celui où les intégrales sont plus faciles à évaluer. Visualiser la région d'intégration peut aider.
  • Quand utiliser les coordonnées cylindriques ou sphériques?

    Utilisez les coordonnées cylindriques pour les régions ayant une symétrie autour d'un axe (par exemple, les cylindres ou les cônes). Utilisez les coordonnées sphériques pour les régions ayant une symétrie autour d'un point (par exemple, les sphères).
  • Que signifie dA et dV dans les intégrales doubles et triples?

    dA représente l'élément d'aire dans le plan xy (dx dy ou dy dx). dV représente l'élément de volume dans l'espace (dx dy dz, dy dx dz, etc.).