Nombre dérivé et tangente : Cours et exercices

Introduction au nombre dérivé

Le nombre dérivé est une notion fondamentale en analyse. Il permet de mesurer la vitesse à laquelle une fonction varie en un point donné. Imaginez une voiture qui roule : le nombre dérivé représente sa vitesse instantanée à un moment précis.

Définition du nombre dérivé

Soit f une fonction définie sur un intervalle I et a un nombre réel appartenant à I. On dit que f est dérivable en a si la limite suivante existe et est finie:

lim (h -> 0) [f(a + h) - f(a)] / h

Cette limite, si elle existe, est appelée le nombre dérivé de f en a et est notée f'(a). La quantité [f(a + h) - f(a)] / h est appelée taux d'accroissement de f entre a et a + h. Pensez à 'h' comme un tout petit changement dans la valeur de x. La fonction est dérivable en 'a' seulement si ce taux s'approche d'une valeur fixe quand 'h' devient de plus en plus petit.

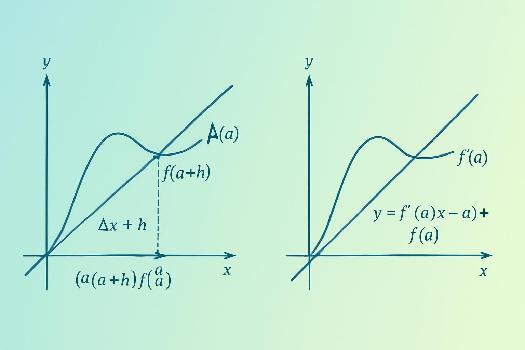
Interprétation géométrique : la tangente

Le nombre dérivé f'(a) représente la pente de la tangente à la courbe représentative de f au point d'abscisse a. La tangente est la droite qui « frôle » la courbe au point (a, f(a)). Si f'(a) est positif, la tangente « monte » ; si f'(a) est négatif, elle « descend » ; et si f'(a) est nul, la tangente est horizontale. L'équation de la tangente à la courbe de f au point d'abscisse a est donnée par :

y = f'(a)(x - a) + f(a)

Exemples de calculs de nombres dérivés

Exemple 1: Soit f(x) = x². Calculons f'(2).

f'(2) = lim (h -> 0) [(2 + h)² - 2²] / h = lim (h -> 0) [4 + 4h + h² - 4] / h = lim (h -> 0) [4h + h²] / h = lim (h -> 0) [4 + h] = 4

Donc, f'(2) = 4. La tangente à la courbe de f(x) = x² au point d'abscisse 2 a pour équation y = 4(x - 2) + 4, soit y = 4x - 4.

Exemple 2: Soit f(x) = 3x + 1. Calculons f'(x).

f'(x) = lim (h -> 0) [3(x + h) + 1 - (3x + 1)] / h = lim (h -> 0) [3x + 3h + 1 - 3x - 1] / h = lim (h -> 0) [3h] / h = lim (h -> 0) 3 = 3

Donc, f'(x) = 3 pour tout x. La fonction est une droite et la pente est constante et égale à 3.

Applications du nombre dérivé

Le nombre dérivé a de nombreuses applications :

• Étude des variations d'une fonction: Le signe du nombre dérivé indique si la fonction est croissante (f'(x) > 0), décroissante (f'(x) < 0) ou constante (f'(x) = 0).
• Recherche d'extremums: Les points où f'(x) = 0 sont des candidats pour être des maximums ou des minimums locaux de la fonction.
• Optimisation: Trouver la valeur qui maximise ou minimise une fonction. Par exemple, trouver les dimensions d'un rectangle de périmètre donné qui a une aire maximale.
• Physique: Calcul de la vitesse et de l'accélération. Si la position d'un objet est donnée par une fonction du temps, sa vitesse est la dérivée de cette fonction par rapport au temps, et son accélération est la dérivée de la vitesse par rapport au temps.

Ce qu'il faut retenir

• Le nombre dérivé f'(a) mesure la variation instantanée d'une fonction f en un point a.
• f'(a) est la limite du taux d'accroissement de f entre a et a + h lorsque h tend vers 0.
• Géométriquement, f'(a) est la pente de la tangente à la courbe de f au point d'abscisse a.
• L'équation de la tangente est y = f'(a)(x - a) + f(a).
• Le signe de f'(x) indique le sens de variation de f.