Mathématiques > Géométrie > Géométrie Spatiale > Orthogonalité de droites et de plans

Orthogonalité de Deux Droites dans l'Espace

Comprendre et démontrer l'orthogonalité de deux droites dans l'espace. Ce guide est conçu pour les lycéens et propose une approche claire et structurée, avec des exemples et des applications.

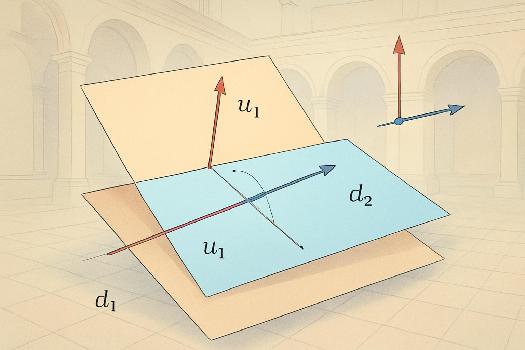
Définition d'orthogonalité de deux droites dans l'espace

Deux droites (d1) et (d2) sont dites orthogonales si leurs directions sont perpendiculaires. Plus précisément, si u1 est un vecteur directeur de (d1) et u2 est un vecteur directeur de (d2), alors (d1) et (d2) sont orthogonales si et seulement si u1 · u2 = 0 (leur produit scalaire est nul). Important : Deux droites orthogonales ne sont pas nécessairement coplanaires (c'est-à-dire qu'elles ne sont pas obligatoirement dans le même plan). Si elles sont coplanaires, alors elles sont perpendiculaires.

Méthode de vérification de l'orthogonalité

Pour vérifier si deux droites sont orthogonales, suivez ces étapes :

  1. Identifier les vecteurs directeurs des deux droites : u1 et u2.
  2. Calculer le produit scalaire des vecteurs directeurs : u1 · u2. Si u1(x1, y1, z1) et u2(x2, y2, z2), alors u1 · u2 = x1x2 + y1y2 + z1z2.
  3. Conclure : Si le produit scalaire est égal à 0, alors les droites sont orthogonales.
Exemple : Soient les droites (d1) de vecteur directeur u1(1, -1, 0) et (d2) de vecteur directeur u2(1, 1, 2). Calculons le produit scalaire : u1 · u2 = (1)(1) + (-1)(1) + (0)(2) = 1 - 1 + 0 = 0. Donc, les droites (d1) et (d2) sont orthogonales.

Orthogonalité et Perpendicularité

La perpendicularité est un cas particulier de l'orthogonalité. Deux droites sont perpendiculaires si elles sont orthogonales et sécantes (c'est-à-dire qu'elles se coupent en un point). Pour vérifier si deux droites sont perpendiculaires, il faut donc vérifier deux conditions :

  1. Orthogonalité : Le produit scalaire de leurs vecteurs directeurs doit être nul.
  2. Sécantes : Les droites doivent avoir un point d'intersection commun. Pour le vérifier, on peut résoudre le système d'équations des deux droites et vérifier s'il existe une solution (un point d'intersection).

Relation entre orthogonalité et plans

Si une droite (d) est orthogonale à deux droites sécantes d'un plan (P), alors (d) est orthogonale à ce plan (P). C'est une propriété fondamentale pour établir l'orthogonalité entre une droite et un plan.

Applications pratiques

L'orthogonalité de deux droites intervient dans :

  • Géométrie 3D : Construction de figures, calcul de distances et d'angles.
  • Physique : Décomposition de forces, étude des mouvements.
  • Infographie : Modélisation d'objets, rendu d'images.
  • Robotique : Planification de trajectoires, contrôle de mouvements.

Ce qu'il faut retenir

  • Deux droites (d1) et (d2) sont orthogonales si leurs vecteurs directeurs u1 et u2 vérifient u1 · u2 = 0.
  • Deux droites perpendiculaires sont orthogonales et sécantes.
  • L'orthogonalité n'implique pas la coplanarité.
  • Si une droite est orthogonale à deux droites sécantes d'un plan, elle est orthogonale à ce plan.

← Maîtriser les valeurs remarquables des fonctions trigonométriques Orthogonalité de Droites et de Plans dans l'Espace →

FAQ

  • Quelle est la différence entre orthogonalité et perpendicularité ?

    Deux droites sont orthogonales si leurs directions sont perpendiculaires (produit scalaire nul des vecteurs directeurs). Si, en plus, elles se coupent, elles sont perpendiculaires.
  • Comment trouver le vecteur directeur d'une droite à partir de son équation paramétrique ?

    Dans l'équation paramétrique d'une droite, les coefficients de 't' (le paramètre) forment le vecteur directeur.
  • Deux droites parallèles peuvent-elles être orthogonales ?

    Non, deux droites parallèles ont le même vecteur directeur (ou des vecteurs directeurs colinéaires). Leur produit scalaire ne peut donc pas être nul, sauf si les vecteurs directeurs sont nuls, ce qui est impossible par définition.