Relations Trigonométriques Fondamentales : Un Guide Détaillé

Introduction aux Relations Trigonométriques

Les relations trigonométriques fondamentales sont les piliers de la trigonométrie. Elles établissent des liens essentiels entre les fonctions trigonométriques (sinus, cosinus, tangente) et permettent de résoudre une multitude de problèmes en géométrie et dans d'autres domaines. Ce guide vous expliquera en détail ces relations, avec des exemples et des illustrations pour une compréhension optimale.

Définition des Fonctions Trigonométriques

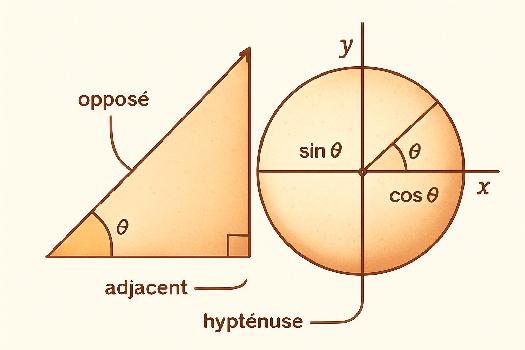
Avant d'explorer les relations, rappelons brièvement les définitions des fonctions trigonométriques dans un triangle rectangle :

1. Sinus (sin) : Le sinus d'un angle aigu est le rapport du côté opposé à cet angle sur l'hypoténuse. sin(θ) = côté opposé / hypotonuse
2. Cosinus (cos) : Le cosinus d'un angle aigu est le rapport du côté adjacent à cet angle sur l'hypoténuse. cos(θ) = côté adjacent / hypotonuse
3. Tangente (tan) : La tangente d'un angle aigu est le rapport du côté opposé à cet angle sur le côté adjacent. tan(θ) = côté opposé / côté adjacent. Elle peut aussi être définie comme le rapport du sinus sur le cosinus : tan(θ) = sin(θ) / cos(θ)

La Relation Fondamentale : sin²(θ) + cos²(θ) = 1

C'est la relation la plus importante et la plus utilisée en trigonométrie. Elle découle directement du théorème de Pythagore appliqué au cercle trigonométrique. Voici une démonstration : Dans un cercle trigonométrique (cercle de rayon 1 centré à l'origine d'un repère), pour tout angle θ, le point sur le cercle a pour coordonnées (cos(θ), sin(θ)). Le théorème de Pythagore nous dit que : cos²(θ) + sin²(θ) = 1² = 1 Conséquences :

• Si vous connaissez la valeur de sin(θ), vous pouvez trouver cos(θ) : cos(θ) = ±√(1 - sin²(θ))
• Si vous connaissez la valeur de cos(θ), vous pouvez trouver sin(θ) : sin(θ) = ±√(1 - cos²(θ))
• Le signe dépend du quadrant dans lequel se trouve l'angle θ.

Relation entre Tangente, Sinus et Cosinus

Comme mentionné précédemment, la tangente d'un angle est définie comme le rapport du sinus sur le cosinus : tan(θ) = sin(θ) / cos(θ) Cette relation est extrêmement utile pour convertir entre tangente et sinus/cosinus, et vice-versa. Exemple : Si sin(θ) = 0.5 et cos(θ) = √3/2, alors tan(θ) = 0.5 / (√3/2) = 1/√3 = √3/3

Les Relations Dérivées : 1 + tan²(θ) = 1/cos²(θ) et 1 + cot²(θ) = 1/sin²(θ)

Ces relations peuvent être dérivées de la relation fondamentale sin²(θ) + cos²(θ) = 1 :

1. 1 + tan²(θ) = 1/cos²(θ) : Divisez l'équation sin²(θ) + cos²(θ) = 1 par cos²(θ) : (sin²(θ)/cos²(θ)) + (cos²(θ)/cos²(θ)) = 1/cos²(θ), ce qui donne tan²(θ) + 1 = 1/cos²(θ)
2. 1 + cot²(θ) = 1/sin²(θ) : Divisez l'équation sin²(θ) + cos²(θ) = 1 par sin²(θ) : (sin²(θ)/sin²(θ)) + (cos²(θ)/sin²(θ)) = 1/sin²(θ), ce qui donne 1 + cot²(θ) = 1/sin²(θ) (où cot(θ) est la cotangente, définie comme cos(θ)/sin(θ))

Applications des Relations Trigonométriques Fondamentales

Les relations trigonométriques fondamentales sont utilisées dans de nombreux domaines :

• Résolution de triangles : Si vous connaissez certains côtés et angles d'un triangle, vous pouvez utiliser ces relations pour trouver les autres.
• Navigation : Elles sont utilisées pour calculer des distances et des angles en navigation maritime et aérienne.
• Physique : Elles apparaissent dans l'étude des ondes, des oscillations et de nombreux autres phénomènes physiques.
• Ingénierie : Elles sont utilisées dans la conception de structures, de ponts et de bâtiments.

Conseils pour la Résolution de Problèmes

Voici quelques conseils pour résoudre des problèmes impliquant des relations trigonométriques :

• Identifiez les informations données : Quels côtés, angles ou fonctions trigonométriques sont connus ?
• Choisissez la relation appropriée : Quelle relation relie les informations données à ce que vous cherchez à trouver ?
• Résolvez l'équation : Isolez l'inconnue et calculez sa valeur.
• Vérifiez votre réponse : Votre réponse est-elle logique compte tenu du contexte du problème ?

Ce qu'il faut retenir

• Sinus (sin) : Côté opposé / Hypothénuse
• Cosinus (cos) : Côté adjacent / Hypothénuse
• Tangente (tan) : Côté opposé / Côté adjacent = sin(θ) / cos(θ)
• Relation fondamentale : sin²(θ) + cos²(θ) = 1
• Relations dérivées : 1 + tan²(θ) = 1/cos²(θ) et 1 + cot²(θ) = 1/sin²(θ)
• Ces relations sont fondamentales pour la résolution de triangles et apparaissent dans de nombreuses applications scientifiques et techniques.