Mathématiques > Géométrie > Géométrie Analytique > Utilisation des coordonnées pour résoudre des problèmes géométriques
Résolution de problèmes géométriques avec les coordonnées
Explorez comment les coordonnées peuvent simplifier la résolution de problèmes de géométrie, du calcul de distances à la détermination d'équations de droites et de cercles.
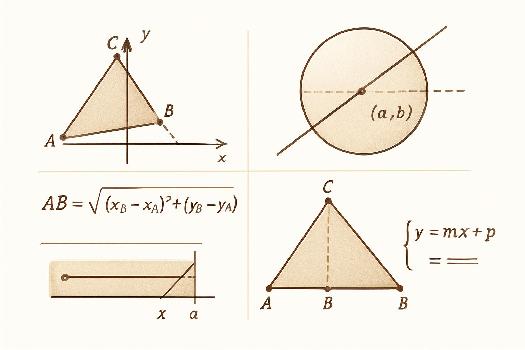
Introduction à la géométrie analytique
La géométrie analytique est une branche des mathématiques qui utilise un système de coordonnées pour étudier les figures géométriques. L'idée fondamentale est de traduire les problèmes géométriques en problèmes algébriques, ce qui permet d'utiliser des équations pour décrire des points, des droites, des cercles et d'autres formes. Ce faisant, nous pouvons appliquer les outils de l'algèbre pour résoudre des problèmes qui seraient beaucoup plus difficiles à aborder avec les méthodes de géométrie pure. L'avantage principal de cette approche est la simplification des raisonnements et la possibilité d'appliquer des formules préétablies.
Calcul de la distance entre deux points
L'une des applications les plus fondamentales des coordonnées est le calcul de la distance entre deux points. Soient deux points A(xA, yA) et B(xB, yB) dans un plan muni d'un repère orthonormé. La distance entre A et B, notée AB, est donnée par la formule :
AB = √((xB - xA)2 + (yB - yA)2)
Exemple: Soient A(1, 2) et B(4, 6). Alors, AB = √((4 - 1)2 + (6 - 2)2) = √(32 + 42) = √(9 + 16) = √25 = 5.
Équation d'une droite
Une droite dans un plan peut être décrite par une équation. La forme générale d'une équation de droite est ax + by + c = 0, où a, b et c sont des constantes réelles et a et b ne sont pas tous les deux nuls. Cependant, la forme la plus couramment utilisée est la forme réduite, qui est y = mx + p, où m est la pente de la droite et p est l'ordonnée à l'origine.
* Pente (m): La pente représente la variation de y pour une variation unitaire de x. Elle indique l'inclinaison de la droite.
* Ordonnée à l'origine (p): L'ordonnée à l'origine est la valeur de y lorsque x = 0. C'est le point où la droite coupe l'axe des ordonnées.
Pour trouver l'équation d'une droite passant par deux points A(xA, yA) et B(xB, yB), on calcule d'abord la pente m = (yB - yA) / (xB - xA), puis on utilise l'un des points pour trouver p en utilisant l'équation y = mx + p.
Équation d'un cercle
Un cercle de centre C(a, b) et de rayon r peut être décrit par l'équation :
(x - a)2 + (y - b)2 = r2
Cette équation exprime le fait que la distance de tout point (x, y) du cercle au centre C(a, b) est égale au rayon r.
Exemple: Un cercle de centre (2, -3) et de rayon 4 a pour équation (x - 2)2 + (y + 3)2 = 16.
Pour déterminer si un point donné appartient au cercle, il suffit de vérifier si ses coordonnées satisfont l'équation du cercle.
Résolution de problèmes : Points d'intersection
La géométrie analytique est particulièrement utile pour trouver les points d'intersection entre différentes figures géométriques. Par exemple, pour trouver les points d'intersection entre une droite et un cercle, on résout le système d'équations formé par l'équation de la droite et l'équation du cercle. Cela peut impliquer de substituer l'expression de y (ou x) de l'équation de la droite dans l'équation du cercle, ce qui conduit à une équation du second degré. Les solutions de cette équation donnent les abscisses des points d'intersection. On peut ensuite trouver les ordonnées correspondantes en utilisant l'équation de la droite. Exemple : Trouver les points d'intersection entre le cercle d'équation x2 + y2 = 25 et la droite d'équation y = x + 1. On substitue y par x + 1 dans l'équation du cercle : x2 + (x + 1)2 = 25, ce qui donne x2 + x2 + 2x + 1 = 25, soit 2x2 + 2x - 24 = 0, ou encore x2 + x - 12 = 0. Les solutions de cette équation sont x = 3 et x = -4. Les points d'intersection sont donc (3, 4) et (-4, -3).
Calcul d'aires
Les coordonnées permettent également de calculer l'aire de figures géométriques. Par exemple, l'aire d'un triangle dont les sommets sont A(xA, yA), B(xB, yB) et C(xC, yC) peut être calculée en utilisant la formule :
Aire = 1/2 * |xA(yB - yC) + xB(yC - yA) + xC(yA - yB)|
Cette formule est particulièrement utile lorsque les sommets du triangle sont donnés par leurs coordonnées.
Ce qu'il faut retenir
- Distance entre deux points :
AB = √((xB - xA)2 + (yB - yA)2) - Équation d'une droite :
y = mx + p(m = pente, p = ordonnée à l'origine) - Équation d'un cercle :
(x - a)2 + (y - b)2 = r2(centre (a, b), rayon r) - Les systèmes d'équations permettent de trouver les points d'intersection entre des figures géométriques.
- L'aire d'un triangle de sommets A, B, C se calcule avec les coordonnées de chaque point.
FAQ
-
Comment trouver l'équation d'une droite si je connais seulement un point et la pente ?
Si vous connaissez un point A(xA, yA) et la pente m, vous pouvez utiliser la forme point-pente de l'équation de la droite :y - yA = m(x - xA). Ensuite, vous pouvez réécrire cette équation sous la forme y = mx + p pour trouver l'ordonnée à l'origine p. -
Comment savoir si deux droites sont parallèles ou perpendiculaires ?
Deux droites sont parallèles si elles ont la même pente (m1 = m2). Elles sont perpendiculaires si le produit de leurs pentes est égal à -1 (m1 * m2 = -1). -
Est-ce que toutes les équations du second degré représentent un cercle ?
Non, pour qu'une équation du second degré représente un cercle, elle doit être de la forme (x - a)2 + (y - b)2 = r2. En particulier, les coefficients de x2 et y2 doivent être égaux à 1, et il ne doit pas y avoir de terme en xy.
