Mathématiques > Algèbre > Fonctions > Fonctions quadratiques

Forme canonique d'une fonction quadratique

Découvrez la forme canonique d'une fonction quadratique, comment la déterminer, et comment l'utiliser pour trouver le sommet et l'axe de symétrie de la parabole.

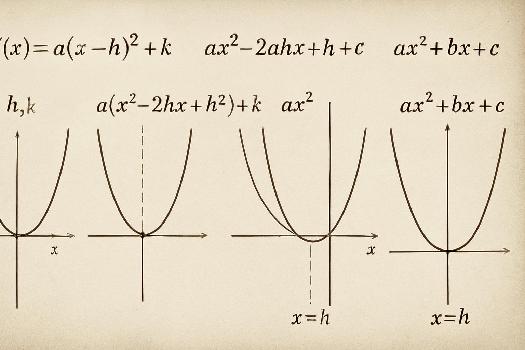
Introduction aux fonctions quadratiques

Les fonctions quadratiques, également appelées fonctions polynômes du second degré, sont des fonctions de la forme f(x) = ax2 + bx + c, où a, b et c sont des nombres réels et a ≠ 0. Leur représentation graphique est une parabole. Comprendre la forme canonique permet d'analyser rapidement les propriétés de cette parabole.

Définition de la forme canonique

La forme canonique d'une fonction quadratique est exprimée comme f(x) = a(x - h)2 + k, où :

  • a est le même coefficient que dans la forme générale (ax2 + bx + c).
  • (h, k) sont les coordonnées du sommet de la parabole.
La forme canonique est particulièrement utile car elle révèle directement les coordonnées du sommet de la parabole et permet de déterminer facilement si la parabole est orientée vers le haut (a > 0) ou vers le bas (a < 0).

Comment déterminer la forme canonique

Il existe deux méthodes principales pour convertir une fonction quadratique de sa forme générale à sa forme canonique:

  1. Complétion du carré:

    Cette méthode consiste à manipuler algébriquement l'expression ax2 + bx + c pour obtenir la forme a(x - h)2 + k.

    Exemple : Convertissons f(x) = x2 + 6x + 5 à la forme canonique.

    1. Factorisez a (ici, a = 1, donc pas de factorisation nécessaire) : f(x) = x2 + 6x + 5
    2. Ajoutez et soustrayez (b/2)2 (ici, (6/2)2 = 9) : f(x) = x2 + 6x + 9 - 9 + 5
    3. Regroupez les trois premiers termes pour former un carré parfait : f(x) = (x + 3)2 - 9 + 5
    4. Simplifiez : f(x) = (x + 3)2 - 4

    Donc, la forme canonique est f(x) = (x + 3)2 - 4. Le sommet est (-3, -4).

  2. Utilisation des formules:

    Vous pouvez utiliser les formules suivantes pour trouver h et k directement:

    • h = -b / (2a)
    • k = f(h) = c - (b2 / (4a))

    Exemple : Convertissons f(x) = 2x2 - 8x + 6 à la forme canonique.

    • h = -(-8) / (2 * 2) = 2
    • k = f(2) = 2(2)2 - 8(2) + 6 = 8 - 16 + 6 = -2

    Donc, la forme canonique est f(x) = 2(x - 2)2 - 2. Le sommet est (2, -2).

Interprétation de la forme canonique

Une fois que vous avez la forme canonique f(x) = a(x - h)2 + k, vous pouvez facilement déterminer les caractéristiques suivantes de la parabole:

  • Sommet: Le sommet de la parabole est le point (h, k). Il représente le minimum (si a > 0) ou le maximum (si a < 0) de la fonction.
  • Axe de symétrie: L'axe de symétrie est la droite verticale passant par le sommet, son équation est x = h.
  • Ouverture de la parabole: Si a > 0, la parabole est ouverte vers le haut. Si a < 0, la parabole est ouverte vers le bas. La valeur absolue de a détermine l'étroitesse ou la largeur de la parabole.

Exemples supplémentaires

Voici quelques exemples supplémentaires pour illustrer la conversion à la forme canonique et l'interprétation des résultats:

  1. Exemple 1: f(x) = -x2 + 4x - 1

    En complétant le carré ou en utilisant les formules, on obtient la forme canonique : f(x) = -(x - 2)2 + 3.

    Le sommet est (2, 3), l'axe de symétrie est x = 2, et la parabole est ouverte vers le bas (a = -1).

  2. Exemple 2: f(x) = 3x2 + 12x + 7

    En complétant le carré ou en utilisant les formules, on obtient la forme canonique : f(x) = 3(x + 2)2 - 5.

    Le sommet est (-2, -5), l'axe de symétrie est x = -2, et la parabole est ouverte vers le haut (a = 3).

Ce qu'il faut retenir

  • La forme canonique d'une fonction quadratique est f(x) = a(x - h)2 + k.
  • (h, k) représente le sommet de la parabole.
  • x = h est l'équation de l'axe de symétrie.
  • a détermine l'ouverture de la parabole (vers le haut si a > 0, vers le bas si a < 0).
  • Deux méthodes pour trouver la forme canonique : Complétion du carré et utilisation des formules h = -b / (2a) et k = f(h).

← Fonctions Paires et Impaires : Comprendre et Identifier Introduction intuitive aux limites de fonctions →

FAQ

  • Pourquoi utiliser la forme canonique plutôt que la forme générale ?

    La forme canonique permet d'identifier rapidement le sommet de la parabole et son axe de symétrie, ce qui facilite l'analyse et la représentation graphique de la fonction.
  • Que signifie si a = 0 dans l'équation f(x) = ax2 + bx + c ?

    Si a = 0, alors la fonction n'est plus une fonction quadratique, mais une fonction linéaire (f(x) = bx + c).
  • Comment trouver les racines (zéros) de la fonction à partir de la forme canonique ?

    Pour trouver les racines, résolvez l'équation a(x - h)2 + k = 0 pour x. Cela peut être plus simple que de résoudre ax2 + bx + c = 0 dans certains cas.