Mathématiques > Géométrie > Trigonométrie > Équations trigonométriques élémentaires

Exemples pratiques de résolution d'équations trigonométriques

Des exemples détaillés et variés pour maîtriser la résolution des équations trigonométriques de base. Chaque exemple est expliqué étape par étape pour une compréhension optimale.

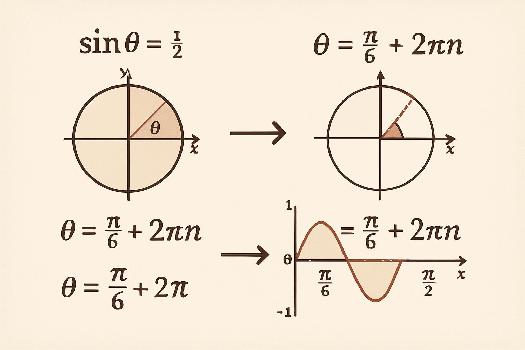
Exemple 1 : Résoudre sin(x) = √3/2

1. Identification : Il s'agit d'une équation de la forme sin(x) = a, avec a = √3/2.

2. Existence : √3/2 est compris entre -1 et 1, donc l'équation a des solutions.

3. Solution particulière : x0 = arcsin(√3/2) = π/3.

4. Solutions générales :
* x = π/3 + 2kπ
* x = (π - π/3) + 2kπ = 2π/3 + 2kπ

où k ∈ ℤ.

Exemple 2 : Résoudre cos(x) = -1/2

1. Identification : Il s'agit d'une équation de la forme cos(x) = a, avec a = -1/2.

2. Existence : -1/2 est compris entre -1 et 1, donc l'équation a des solutions.

3. Solution particulière : x0 = arccos(-1/2) = 2π/3.

4. Solutions générales :
* x = 2π/3 + 2kπ
* x = -2π/3 + 2kπ

où k ∈ ℤ.

Exemple 3 : Résoudre tan(x) = -1

1. Identification : Il s'agit d'une équation de la forme tan(x) = a, avec a = -1.

2. Existence : L'équation a toujours des solutions pour n'importe quelle valeur de 'a'.

3. Solution particulière : x0 = arctan(-1) = -π/4.

4. Solutions générales :
* x = -π/4 + kπ

où k ∈ ℤ. On peut aussi écrire x = 3π/4 + kπ (car -π/4 et 3π/4 sont équivalents à π près).

Exemple 4 : Résoudre 2sin(x) - 1 = 0

1. Transformation : On isole d'abord sin(x): 2sin(x) = 1 => sin(x) = 1/2.

2. Identification : Il s'agit d'une équation de la forme sin(x) = a, avec a = 1/2.

3. Existence : 1/2 est compris entre -1 et 1, donc l'équation a des solutions.

4. Solution particulière : x0 = arcsin(1/2) = π/6.

5. Solutions générales :
* x = π/6 + 2kπ
* x = (π - π/6) + 2kπ = 5π/6 + 2kπ

où k ∈ ℤ.

Exemple 5 : Résoudre √3 cos(x) = 3/2

1. Transformation : On isole d'abord cos(x): cos(x) = (3/2) / √3 => cos(x) = √3/2.

2. Identification : Il s'agit d'une équation de la forme cos(x) = a, avec a = √3/2.

3. Existence : √3/2 est compris entre -1 et 1, donc l'équation a des solutions.

4. Solution particulière : x0 = arccos(√3/2) = π/6.

5. Solutions générales :
* x = π/6 + 2kπ
* x = -π/6 + 2kπ

où k ∈ ℤ.

Ce qu'il faut retenir

  • Toujours isoler la fonction trigonométrique (sin, cos, tan) avant de trouver la solution particulière.
  • Appliquer les formules générales en tenant compte de la périodicité et des symétries.
  • Simplifier les solutions et vérifier leur validité.
  • Ne pas hésiter à transformer l'équation pour la ramener à une forme connue.

← Démonstration et applications avancées de la distance entre deux points Exercices Corrigés : Maîtriser les Angles Orientés et les Radians →

FAQ

  • Que faire si l'équation contient d'autres termes (ex: 2sin(x) + 1 = 0) ?

    Il faut isoler la fonction trigonométrique avant d'appliquer les méthodes de résolution classiques. Dans cet exemple, il faut d'abord écrire sin(x) = -1/2.
  • Comment vérifier si une solution est correcte ?

    Remplacez la solution trouvée dans l'équation d'origine et vérifiez si l'équation est satisfaite.