Représentation graphique de la fonction tangente

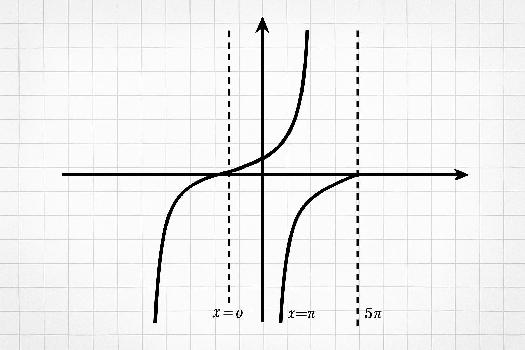
Introduction à la fonction tangente

La fonction tangente, notée y = tan(x), est une autre fonction trigonométrique fondamentale. Elle est définie comme le rapport du sinus au cosinus : tan(x) = sin(x) / cos(x). Sa représentation graphique est différente de celles du sinus et du cosinus, notamment à cause de ses asymptotes.

La fonction tangente est définie à partir du cercle trigonométrique. Pour un angle θ (thêta), la tangente de θ est l'ordonnée du point d'intersection entre la droite passant par l'origine et le point du cercle trigonométrique correspondant à l'angle θ, et la droite verticale passant par le point (1,0). (Abscisse égale à 1).

Caractéristiques de la fonction tangente : y = tan(x)

La fonction tangente a une allure particulière, caractérisée par des asymptotes verticales. Sa principale caractéristique est sa périodicité. La période de la tangente est π (environ 3.14), ce qui signifie que le motif de la courbe se répète tous les π radians.

• Asymptotes : La fonction tangente tend vers l'infini lorsque x approche π/2 + kπ, où k est un entier. Ces valeurs correspondent aux points où cos(x) = 0. Ce sont des asymptotes verticales.
• Zéros : La fonction tangente s'annule (y = 0) aux multiples entiers de π (0, π, 2π, 3π, ...). C'est là où sin(x) = 0.
• Comportement : La fonction tangente est croissante sur chaque intervalle où elle est définie. Elle prend toutes les valeurs réelles entre -∞ et +∞.

Pour tracer la courbe, il est important de bien positionner les asymptotes et de connaître le comportement de la fonction entre ces asymptotes. Elle passe par zéro à chaque multiple de π et tend vers l'infini de part et d'autre des asymptotes.

Transformations de la fonction tangente

Comme pour le sinus et le cosinus, il est possible de transformer la fonction tangente. Ces transformations modifient sa période et son comportement autour des asymptotes.

• Période : La fonction y = tan(Bx) a une période de π/|B|. Si B est supérieur à 1, la période est réduite, ce qui signifie que la courbe est comprimée horizontalement. Si B est inférieur à 1, la période est augmentée, ce qui signifie que la courbe est étirée horizontalement.
• Facteur d'échelle vertical : La fonction y = A tan(x) modifie la pente de la courbe. Si A est supérieur à 1, la courbe est plus raide. Si A est inférieur à 1, la courbe est moins raide. Si A est négatif, la courbe est inversée par rapport à l'axe des x.
• Déphasage : La fonction y = tan(x - C) est déphasée de C unités. Si C est positif, la courbe est décalée vers la droite. Si C est négatif, la courbe est décalée vers la gauche.
• Déplacement vertical : La fonction y = tan(x) + D est décalée verticalement de D unités. Si D est positif, la courbe est déplacée vers le haut. Si D est négatif, la courbe est déplacée vers le bas.

Exemples concrets

Voici quelques exemples de transformations de la fonction tangente :

• y = 2tan(x) : La courbe est plus raide.
• y = tan(2x) : Période divisée par 2. Les asymptotes sont plus rapprochées.
• y = tan(x - π/4) : Déphasage de π/4 vers la droite.
• y = tan(x) + 1 : Déplacement vertical de 1 unité vers le haut.
• y = -tan(x) : La courbe est inversée par rapport à l'axe des x.

Ce qu'il faut retenir

• Fonction tangente : Définie comme sin(x) / cos(x).
• Période : π.
• Asymptotes verticales : x = π/2 + kπ, où k est un entier.
• Zéros : Multiples entiers de π.
• Transformations : Modifications de la période, du facteur d'échelle vertical, du déphasage et du déplacement vertical.

La fonction tangente est utilisée dans de nombreux domaines, notamment en trigonométrie, en géométrie et en physique, pour modéliser des phénomènes périodiques avec des asymptotes.