Mathématiques > Probabilités et Statistiques > Statistiques > Analyse de données

Analyse de la variance (ANOVA)

Comprendre et appliquer l'analyse de la variance (ANOVA) pour comparer les moyennes de plusieurs groupes. Ce guide détaillé explique les concepts clés, les étapes du calcul et l'interprétation des résultats.

Introduction à l'ANOVA

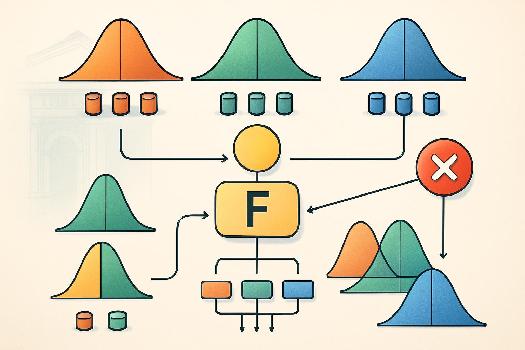
L'analyse de la variance (ANOVA) est une méthode statistique utilisée pour comparer les moyennes de deux ou plusieurs groupes. Contrairement aux tests t qui comparent seulement deux groupes, l'ANOVA peut analyser simultanément plusieurs groupes, ce qui est essentiel lorsque vous avez plus de deux conditions ou traitements à comparer. L'ANOVA teste si les variations entre les groupes sont significativement plus importantes que les variations à l'intérieur de chaque groupe. En d'autres termes, elle détermine si les différences observées entre les moyennes des groupes sont dues à un effet réel ou simplement au hasard.

Hypothèses de l'ANOVA

Pour que l'ANOVA soit applicable, certaines hypothèses doivent être vérifiées :

  • Normalité : Les données de chaque groupe doivent suivre une distribution normale.
  • Homogénéité des variances (Homoscédasticité) : Les variances de tous les groupes doivent être égales. Il existe des tests statistiques pour vérifier cette hypothèse, comme le test de Levene.
  • Indépendance des observations : Les observations dans chaque groupe doivent être indépendantes les unes des autres.
Si ces hypothèses ne sont pas respectées, l'ANOVA peut donner des résultats inexacts. Il existe des alternatives non paramétriques, comme le test de Kruskal-Wallis, qui peuvent être utilisées lorsque l'hypothèse de normalité n'est pas vérifiée.

Calcul de l'ANOVA

Le calcul de l'ANOVA implique plusieurs étapes. Voici un aperçu simplifié :

  1. Calcul de la Somme des Carrés Totale (SCT) : Mesure la variation totale des données.
  2. Calcul de la Somme des Carrés Inter-groupes (SCI) : Mesure la variation entre les moyennes des groupes.
  3. Calcul de la Somme des Carrés Intra-groupes (SCE) : Mesure la variation à l'intérieur de chaque groupe.
  4. Calcul des Degrés de Liberté : Pour SCI (nombre de groupes - 1) et pour SCE (nombre total d'observations - nombre de groupes).
  5. Calcul des Carrés Moyens : SCI divisé par ses degrés de liberté et SCE divisé par ses degrés de liberté.
  6. Calcul de la Statistique F : Carré Moyen Inter-groupes divisé par Carré Moyen Intra-groupes.
La statistique F est ensuite comparée à une valeur critique de la distribution F pour déterminer la signification statistique.

Interprétation des résultats

Une fois la statistique F calculée, vous la comparez à une valeur critique de la distribution F, basée sur vos degrés de liberté et votre niveau de signification (généralement α = 0.05). Si la statistique F est supérieure à la valeur critique, vous rejetez l'hypothèse nulle (H0) et concluez qu'il existe une différence significative entre au moins deux des moyennes des groupes. Il est crucial de comprendre que l'ANOVA vous dit seulement qu'il y a une différence significative, mais ne vous dit pas quels groupes sont différents les uns des autres. Pour cela, vous devez effectuer des tests post-hoc (comme le test de Tukey ou le test de Bonferroni) pour comparer les paires de groupes et identifier les différences spécifiques.

Exemple concret

Supposons que vous voulez comparer l'efficacité de trois méthodes d'enseignement des mathématiques : la méthode A, la méthode B et la méthode C. Vous divisez une classe en trois groupes, chacun utilisant une méthode différente. Après une période d'enseignement, vous administrez un test à tous les élèves.

  • Hypothèse nulle (H0) : Les moyennes des scores des trois groupes sont égales.
  • Hypothèse alternative (H1) : Au moins deux des moyennes des scores des trois groupes sont différentes.
Après avoir effectué l'ANOVA, vous obtenez une statistique F de 5.20 et une valeur p de 0.01. Étant donné que la valeur p est inférieure à 0.05, vous rejetez l'hypothèse nulle et concluez qu'il existe une différence significative entre au moins deux des méthodes d'enseignement. Vous effectuez ensuite des tests post-hoc pour déterminer quelles méthodes sont significativement différentes.

Ce qu'il faut retenir

  • L'ANOVA est utilisée pour comparer les moyennes de plusieurs groupes.
  • Les hypothèses de normalité, d'homogénéité des variances et d'indépendance doivent être vérifiées.
  • La statistique F est utilisée pour déterminer la signification statistique.
  • Les tests post-hoc sont nécessaires pour identifier les différences spécifiques entre les groupes après avoir rejeté l'hypothèse nulle.
  • L'ANOVA est une technique puissante pour l'analyse de données expérimentales et observationnelles.

← Comprendre et Interpréter les Représentations Graphiques: Histogrammes, Diagrammes Circulaires et Boîtes à Moustaches →

FAQ

  • Quelle est la différence entre un test t et une ANOVA ?

    Un test t est utilisé pour comparer les moyennes de deux groupes, tandis que l'ANOVA est utilisée pour comparer les moyennes de deux ou plusieurs groupes.
  • Que se passe-t-il si les hypothèses de l'ANOVA ne sont pas respectées ?

    Si les hypothèses de l'ANOVA ne sont pas respectées, les résultats peuvent être inexacts. Des alternatives non paramétriques, comme le test de Kruskal-Wallis, peuvent être utilisées.
  • Que sont les tests post-hoc et pourquoi sont-ils nécessaires ?

    Les tests post-hoc sont des tests supplémentaires effectués après l'ANOVA pour identifier les différences spécifiques entre les groupes lorsque l'ANOVA a montré une différence significative globale.