Comprendre les Limites de Fonctions en un Point

Définition Intuitive

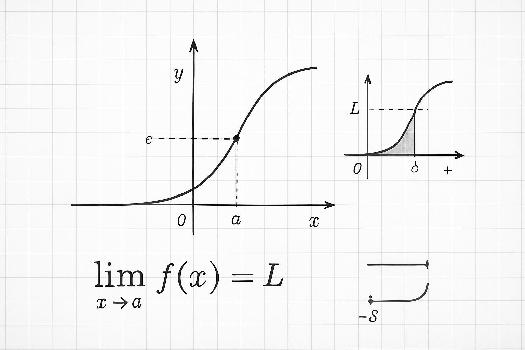
La limite d'une fonction f(x) en un point a, notée lim_x→a f(x), est la valeur vers laquelle f(x) se rapproche lorsque x se rapproche de a. Il est crucial de comprendre que x ne prend jamais la valeur de a, mais s'en approche infiniment près. On peut dire que si on prend des valeurs de x de plus en plus proches de a, les valeurs correspondantes de f(x) se rapprochent de plus en plus d'une certaine valeur L, alors L est la limite de f(x) en a.

Définition Formelle (ε-δ)

La définition formelle de la limite, utilisant les epsilon (ε) et delta (δ), est la suivante : pour tout ε > 0, il existe un δ > 0 tel que si 0 < |x - a| < δ, alors |f(x) - L| < ε. Cette définition, bien que plus abstraite, permet de prouver rigoureusement l'existence et la valeur d'une limite. Elle signifie qu'on peut rendre f(x) aussi proche que l'on veut de L (à ε près) en choisissant x suffisamment proche de a (à δ près).

Calcul des Limites : Méthodes Directes

• Substitution Directe: Si f(x) est continue en x = a, alors lim_x→a f(x) = f(a). Par exemple, lim_x→2 (x² + 1) = 2² + 1 = 5.
• Simplification: Si la substitution directe donne une forme indéterminée (0/0, ∞/∞, etc.), on peut essayer de simplifier l'expression avant de substituer. Cela peut inclure la factorisation, la rationalisation, ou l'utilisation d'identités trigonométriques.

Formes Indéterminées et Techniques de Résolution

Plusieurs formes indéterminées peuvent apparaître lors du calcul des limites. Les plus courantes sont 0/0, ∞/∞, ∞ - ∞, 0 * ∞, 1^∞, 0⁰, et ∞⁰. Pour les résoudre, on utilise différentes techniques:

• Factorisation et Simplification: Utile pour les expressions polynomiales.
• Rationalisation: Utile pour les expressions contenant des racines carrées. Multiplier par la quantité conjuguée.
• Règle de l'Hôpital: Si la limite est de la forme 0/0 ou ∞/∞, on peut dériver le numérateur et le dénominateur séparément et recalculer la limite.
• Changement de Variable: Peut simplifier l'expression en introduisant une nouvelle variable.

Limites Unilatérales

Les limites unilatérales considèrent la limite lorsque x approche a par la gauche (lim_x→a^- f(x)) ou par la droite (lim_x→a⁺ f(x)). Pour qu'une limite existe en a, les limites unilatérales doivent exister et être égales. Si lim_x→a^- f(x) = lim_x→a⁺ f(x) = L, alors lim_x→a f(x) = L.

Exemples Concrets

Exemple 1: Calculer lim_x→2 (x² - 4) / (x - 2). Substitution directe donne 0/0. Factorisons: (x² - 4) / (x - 2) = (x - 2)(x + 2) / (x - 2) = x + 2. Donc, lim_x→2 (x² - 4) / (x - 2) = lim_x→2 (x + 2) = 2 + 2 = 4. Exemple 2: Calculer lim_x→0 sin(x) / x. C'est une limite fondamentale. On peut démontrer (par exemple, en utilisant la règle de L'Hôpital) que lim_x→0 sin(x) / x = 1. Exemple 3: Calculer lim_x→1⁺ 1 / (x - 1). Lorsque x approche 1 par la droite, (x - 1) approche 0 par des valeurs positives. Donc, la limite est +∞.

Ce qu'il faut retenir

• La limite d'une fonction f(x) en x = a décrit le comportement de f(x) lorsque x s'approche de a.
• La substitution directe est la première méthode à essayer, mais peut mener à des formes indéterminées.
• Les formes indéterminées (0/0, ∞/∞, etc.) nécessitent des techniques de simplification (factorisation, rationalisation, règle de l'Hôpital).
• Les limites unilatérales (à gauche et à droite) doivent être égales pour que la limite existe.
• La définition formelle (ε-δ) est la base rigoureuse de la notion de limite.