Mathématiques > Analyse > Intégration > Primitive d'une fonction

Primitive particulière : Trouver la constante d'intégration

Apprenez à déterminer la primitive particulière d'une fonction qui satisfait une condition initiale donnée. Exemples et exercices corrigés.

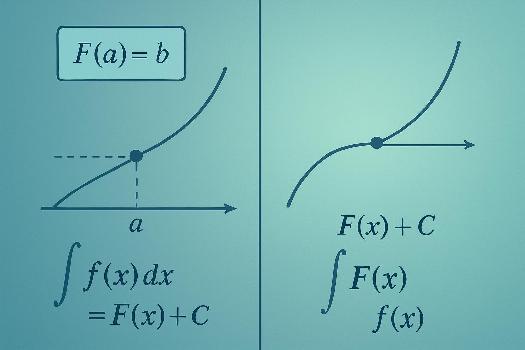
La constante d'intégration

On sait qu'une fonction possède une infinité de primitives qui diffèrent par une constante. Cette constante, notée C, est appelée la constante d'intégration. Pour déterminer une primitive particulière, il faut connaître une information supplémentaire, appelée condition initiale.

Condition initiale

Une condition initiale est une information de la forme F(a) = b, où a et b sont des nombres réels et F(x) est la primitive recherchée. Cette condition nous permet de déterminer la valeur de la constante C.

Méthode pour déterminer la primitive particulière

Voici les étapes à suivre pour déterminer la primitive particulière F(x) d'une fonction f(x) telle que F(a) = b:

  • Calculer la primitive générale F(x) = ∫f(x) dx + C.
  • Utiliser la condition initiale F(a) = b pour déterminer la valeur de C.
  • Remplacer C par sa valeur dans l'expression de F(x).

Exemple 1

Trouver la primitive F(x) de f(x) = x2 telle que F(1) = 2.

  • Calcul de la primitive générale: F(x) = ∫x2 dx = (x3)/3 + C
  • Utilisation de la condition initiale: F(1) = (13)/3 + C = 2. Donc, 1/3 + C = 2, ce qui implique C = 2 - 1/3 = 5/3.
  • La primitive particulière est: F(x) = (x3)/3 + 5/3

Exemple 2

Trouver la primitive F(x) de f(x) = cos(x) telle que F(π/2) = 1.

  • Calcul de la primitive générale: F(x) = ∫cos(x) dx = sin(x) + C
  • Utilisation de la condition initiale: F(π/2) = sin(π/2) + C = 1. Donc, 1 + C = 1, ce qui implique C = 0.
  • La primitive particulière est: F(x) = sin(x)

Importance de la condition initiale

La condition initiale est essentielle pour déterminer une primitive particulière. Sans elle, on ne peut qu'exprimer la primitive sous forme générale, avec une constante d'intégration indéterminée.

Ce qu'il faut retenir

  • Pour déterminer une primitive particulière, il faut une condition initiale de la forme F(a) = b.
  • On calcule la primitive générale, puis on utilise la condition initiale pour trouver la valeur de la constante d'intégration C.
  • Une fois C trouvé, on remplace sa valeur dans l'expression de la primitive générale.

← Opérations sur les limites : Continuité et exemples avancés Primitives d'une fonction : Définition, calcul et exemples →

FAQ

  • La condition initiale est-elle toujours de la forme F(a) = b ?

    Oui, la condition initiale est toujours de cette forme, car elle spécifie la valeur de la primitive en un point donné.
  • Que se passe-t-il si j'ai plusieurs conditions initiales ?

    Si vous avez plusieurs conditions initiales, vous pourriez avoir un système d'équations à résoudre pour trouver plusieurs constantes. Cependant, dans le cadre du lycée, vous n'aurez généralement qu'une seule condition initiale pour déterminer une unique constante d'intégration.