Introduction aux Matrices : Définitions et Vocabulaire Essentiel

Qu'est-ce qu'une Matrice ?

Une matrice est un tableau rectangulaire de nombres (réels ou complexes) agencés en lignes et en colonnes. On utilise généralement des lettres majuscules pour désigner les matrices, par exemple, A, B, C, etc. Les nombres qui composent la matrice sont appelés coefficients ou éléments.

Taille (ou dimension) d'une Matrice

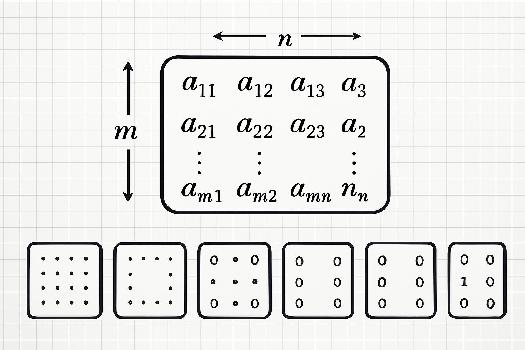
La taille d'une matrice est donnée par son nombre de lignes et son nombre de colonnes. Si une matrice possède m lignes et n colonnes, on dit qu'elle est de taille m x n (on lit « m par n »). L'ordre est important : on indique toujours le nombre de lignes en premier, puis le nombre de colonnes. Par exemple, une matrice 3 x 2 a 3 lignes et 2 colonnes.

Représentation des coefficients

Chaque coefficient d'une matrice est identifié par sa position (ligne, colonne). On utilise la notation a_ij pour désigner l'élément situé à la i-ième ligne et à la j-ième colonne de la matrice A.
Par exemple, si A est une matrice 3 x 2 :

A =

a11	a12
a21	a22
a31	a32

a₁₁ est le coefficient situé à la première ligne et première colonne, a₂₁ est le coefficient situé à la deuxième ligne et première colonne, et ainsi de suite.

Exemples Concrets

Prenons quelques exemples :

Exemple 1: Soit la matrice B =

1	2	3
4	5	6

B est une matrice de taille 2 x 3 (2 lignes et 3 colonnes). Le coefficient b₁₂ est 2 (première ligne, deuxième colonne). Le coefficient b₂₃ est 6 (deuxième ligne, troisième colonne).

Exemple 2: Soit la matrice C =

7

8

9

C est une matrice de taille 3 x 1 (3 lignes et 1 colonne). On l'appelle aussi matrice colonne. Le coefficient c₂₁ est 8 (deuxième ligne, première colonne).

Exemple 3: Soit la matrice D =

-1	0
0	1

D est une matrice de taille 2 x 2 (2 lignes et 2 colonnes). On l'appelle aussi matrice carrée. Le coefficient d₁₁ est -1 (première ligne, première colonne). Le coefficient d₂₂ est 1 (deuxième ligne, deuxième colonne).

Types de Matrices Particulières

Il existe plusieurs types de matrices qui méritent d'être mentionnés :

• Matrice carrée : Une matrice avec le même nombre de lignes et de colonnes (n x n).
• Matrice ligne : Une matrice avec une seule ligne (1 x n).
• Matrice colonne : Une matrice avec une seule colonne (m x 1).
• Matrice nulle : Une matrice dont tous les coefficients sont égaux à zéro.
• Matrice diagonale : Une matrice carrée dont tous les coefficients en dehors de la diagonale principale sont nuls. La diagonale principale est constituée des éléments a_ii (où le numéro de ligne est égal au numéro de colonne).
• Matrice identité : Une matrice diagonale dont tous les coefficients sur la diagonale principale sont égaux à 1. Elle est souvent notée I_n, où n est la taille de la matrice.

Ce qu'il faut retenir

• Une matrice est un tableau de nombres organisés en lignes et colonnes.
• La taille d'une matrice est donnée par le nombre de lignes et de colonnes (m x n).
• Chaque coefficient est identifié par sa position (a_ij : i-ième ligne, j-ième colonne).
• Il existe des types de matrices particulières : carrée, ligne, colonne, nulle, diagonale, identité.