Mathématiques > Algèbre > Suites Numériques > Limites de suites (notion intuitive)

Introduction intuitive aux limites de suites numériques

Explorez la notion de limite d'une suite numérique de manière intuitive et accessible. Comprenez comment une suite peut se rapprocher infiniment d'une valeur spécifique. Découvrez des exemples concrets et des explications détaillées pour maîtriser ce concept essentiel de l'analyse mathématique.

Qu'est-ce qu'une suite numérique ?

Une suite numérique est une liste ordonnée de nombres. Chaque nombre dans la suite est appelé un terme. On peut noter une suite comme (un), où n représente le rang du terme dans la suite (n est généralement un entier naturel). Par exemple: 2, 4, 6, 8, ... est une suite où u1 = 2, u2 = 4, etc. Un autre exemple pourrait être la suite définie par un = n2, dont les premiers termes sont 1, 4, 9, 16, ...

L'idée intuitive de limite

L'idée de limite d'une suite est de comprendre ce qui se passe avec les termes de la suite lorsque 'n' devient très grand. Si les termes de la suite se rapprochent de plus en plus d'une certaine valeur 'L' lorsque 'n' devient infiniment grand, on dit que la suite converge vers 'L', et 'L' est la limite de la suite. Imaginez une cible. Chaque terme de la suite est une flèche lancée vers cette cible. Si, en lançant de plus en plus de flèches (n grandit), les flèches se regroupent de plus en plus près du centre de la cible, alors le centre de la cible est la limite de la suite.

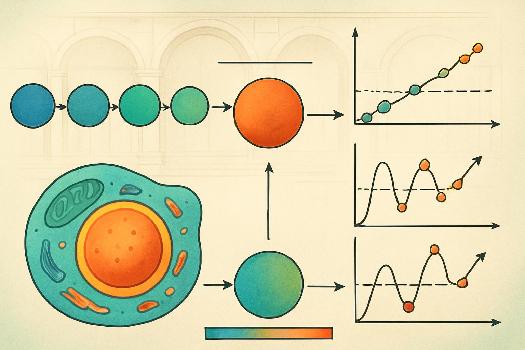
Exemple 1 : Suite convergente

Considérons la suite un = 1/n. Calculons quelques termes : u1 = 1, u2 = 1/2 = 0.5, u3 = 1/3 = 0.333..., u10 = 1/10 = 0.1, u100 = 1/100 = 0.01, u1000 = 1/1000 = 0.001. On observe que lorsque 'n' devient très grand (10, 100, 1000, ...), les termes de la suite se rapprochent de plus en plus de 0. On dit donc que la limite de la suite un = 1/n est 0, et on écrit lim (n->infini) 1/n = 0. Autrement dit, la suite converge vers 0.

Exemple 2 : Suite divergente

Considérons la suite un = n. Calculons quelques termes : u1 = 1, u2 = 2, u3 = 3, u10 = 10, u100 = 100, u1000 = 1000. On observe que lorsque 'n' devient très grand, les termes de la suite deviennent de plus en plus grands et ne se rapprochent pas d'une valeur finie. On dit que la suite un = n diverge vers l'infini. Elle n'a pas de limite finie.

Exemple 3 : Suite oscillante

Considérons la suite un = (-1)n. Calculons quelques termes : u1 = -1, u2 = 1, u3 = -1, u4 = 1, ... On observe que les termes de la suite alternent entre -1 et 1. Ils ne se rapprochent pas d'une valeur unique lorsque 'n' devient grand. On dit que la suite un = (-1)n diverge, mais d'une manière différente de l'exemple précédent. Elle oscille entre deux valeurs et n'a pas de limite.

Importance de la limite

La notion de limite est fondamentale en mathématiques et en particulier en analyse. Elle sert de base pour définir des concepts tels que la continuité, la dérivabilité et l'intégrabilité. La compréhension intuitive des limites est cruciale pour aborder des sujets plus avancés en mathématiques.

Ce qu'il faut retenir

  • Une suite numérique est une liste ordonnée de nombres.
  • La limite d'une suite est la valeur vers laquelle les termes de la suite se rapprochent lorsque l'indice (n) devient infiniment grand.
  • Si une suite a une limite finie, on dit qu'elle converge.
  • Si une suite n'a pas de limite finie, on dit qu'elle diverge. Une suite peut diverger vers l'infini ou osciller.
  • La notion de limite est fondamentale en analyse et permet de définir d'autres concepts importants.

← Introduction intuitive aux limites de fonctions Introduction intuitive à la continuité d'une fonction →

FAQ

  • Comment savoir si une suite converge ou diverge ?

    Il existe différentes méthodes pour déterminer si une suite converge ou diverge. On peut analyser le comportement des termes lorsque 'n' devient grand, utiliser des théorèmes de convergence (comme le théorème des gendarmes), ou étudier les variations de la suite.
  • Toutes les suites ont-elles une limite ?

    Non, toutes les suites n'ont pas une limite. Certaines suites divergent, c'est-à-dire que leurs termes ne se rapprochent pas d'une valeur finie lorsque 'n' devient grand. Ces suites peuvent tendre vers l'infini ou osciller.