Vecteurs dans l'espace : Définition, Opérations et Colinéarité

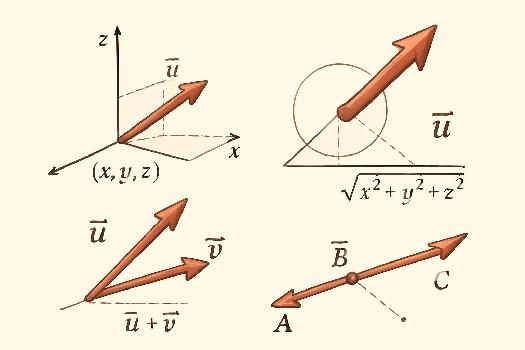
Définition d'un vecteur dans l'espace

Un vecteur dans l'espace est caractérisé par :

• Une direction : la droite sur laquelle il se trouve ou toute droite parallèle.
• Un sens : l'orientation sur cette droite (de A vers B ou de B vers A).
• Une norme : la longueur du segment qui le représente, notée ||AB||.

Représentation d'un vecteur dans un repère orthonormé

Dans un repère orthonormé (O, i, j, k), un vecteur $\backslash vec\{u\}$ peut être défini par ses coordonnées : $\backslash vec\{u\}(x\; ;\; y\; ;\; z)$. x, y et z sont les composantes du vecteur. Si $\backslash vec\{u\}\; =\; \backslash vec\{AB\}$ et A(xA ; yA ; zA) et B(xB ; yB ; zB), alors les coordonnées du vecteur $\backslash vec\{AB\}$ sont : $\backslash vec\{AB\}(xB\; -\; xA\; ;\; yB\; -\; yA\; ;\; zB\; -\; zA)$. La norme du vecteur $\backslash vec\{u\}(x\; ;\; y\; ;\; z)$ est calculée par : $||\backslash vec\{u\}||\; =\; \backslash sqrt\{x^2\; +\; y^2\; +\; z^2\}$.

Opérations sur les vecteurs : Addition

Addition de vecteurs : Si $\backslash vec\{u\}(x\_u\; ;\; y\_u\; ;\; z\_u)$ et $\backslash vec\{v\}(x\_v\; ;\; y\_v\; ;\; z\_v)$, alors $\backslash vec\{u\}\; +\; \backslash vec\{v\}(x\_u\; +\; x\_v\; ;\; y\_u\; +\; y\_v\; ;\; z\_u\; +\; z\_v)$. Géométriquement, on peut utiliser la règle du parallélogramme pour l'addition de deux vecteurs ayant la même origine. On forme un parallélogramme dont les vecteurs sont deux côtés adjacents. La diagonale issue de l'origine représente le vecteur somme. On peut aussi utiliser la relation de Chasles : $\backslash vec\{AB\}\; +\; \backslash vec\{BC\}\; =\; \backslash vec\{AC\}$.

Opérations sur les vecteurs : Multiplication par un scalaire

Multiplication par un scalaire : Si $\backslash vec\{u\}(x\; ;\; y\; ;\; z)$ et k est un nombre réel (scalaire), alors $k\backslash vec\{u\}(kx\; ;\; ky\; ;\; kz)$. Si k > 0, alors $k\backslash vec\{u\}$ a la même direction et le même sens que $\backslash vec\{u\}$, et sa norme est k fois la norme de $\backslash vec\{u\}$. Si k < 0, alors $k\backslash vec\{u\}$ a la même direction mais le sens opposé à $\backslash vec\{u\}$, et sa norme est |k| fois la norme de $\backslash vec\{u\}$.

Colinéarité de deux vecteurs

Deux vecteurs $\backslash vec\{u\}$ et $\backslash vec\{v\}$ sont colinéaires s'il existe un scalaire k tel que $\backslash vec\{u\}\; =\; k\backslash vec\{v\}$. Cela signifie qu'ils ont la même direction (ils sont parallèles). Si $\backslash vec\{u\}(x\_u\; ;\; y\_u\; ;\; z\_u)$ et $\backslash vec\{v\}(x\_v\; ;\; y\_v\; ;\; z\_v)$, alors $\backslash vec\{u\}$ et $\backslash vec\{v\}$ sont colinéaires si et seulement si $x\_u\; =\; kx\_v$, $y\_u\; =\; ky\_v$ et $z\_u\; =\; kz\_v$. On peut également exprimer la colinéarité en vérifiant que les rapports des composantes sont égaux : $\backslash frac\{x\_u\}\{x\_v\}\; =\; \backslash frac\{y\_u\}\{y\_v\}\; =\; \backslash frac\{z\_u\}\{z\_v\}\; =\; k$ (à condition que $x\_v$, $y\_v$ et $z\_v$ soient non nuls). Important: Le vecteur nul est colinéaire à tout vecteur.

Application de la colinéarité : Alignement de points

Trois points A, B et C sont alignés si et seulement si les vecteurs $\backslash vec\{AB\}$ et $\backslash vec\{AC\}$ sont colinéaires. Cela permet de démontrer l'alignement de points dans l'espace en calculant les coordonnées des vecteurs et en vérifiant leur colinéarité.

Ce qu'il faut retenir

• Définition d'un vecteur : Direction, sens, norme.
• Coordonnées d'un vecteur : $\backslash vec\{u\}(x\; ;\; y\; ;\; z)$, où x, y, z sont les composantes dans un repère orthonormé.
• Norme d'un vecteur : $||\backslash vec\{u\}||\; =\; \backslash sqrt\{x^2\; +\; y^2\; +\; z^2\}$.
• Addition de vecteurs : $\backslash vec\{u\}\; +\; \backslash vec\{v\}(x\_u\; +\; x\_v\; ;\; y\_u\; +\; y\_v\; ;\; z\_u\; +\; z\_v)$. Relation de Chasles.
• Multiplication par un scalaire : $k\backslash vec\{u\}(kx\; ;\; ky\; ;\; kz)$.
• Colinéarité : $\backslash vec\{u\}\; =\; k\backslash vec\{v\}$. Rapports des composantes égaux. L'alignement de points A, B, C est équivalent à la colinéarité des vecteurs $\backslash vec\{AB\}$ et $\backslash vec\{AC\}$.