Résolution d'Équations Complexes et Interprétation Géométrique

Introduction aux Équations Complexes

Les équations complexes sont des équations dont l'inconnue est un nombre complexe, généralement noté z. Résoudre une équation complexe consiste à trouver toutes les valeurs de z qui vérifient l'équation. Contrairement aux équations réelles, les solutions des équations complexes peuvent être des nombres réels, imaginaires purs, ou des nombres complexes généraux de la forme a + bi, où a et b sont des nombres réels et i est l'unité imaginaire (i² = -1).

Équations du Premier Degré

Les équations du premier degré en z ont la forme az + b = 0, où a et b sont des nombres complexes et a ≠ 0. La solution est donnée par z = -b/a. Pour trouver la solution, il suffit d'effectuer la division de nombres complexes. Exemple: Résolvons l'équation (1 + i)z + 2 - i = 0. z = -(2 - i) / (1 + i). Pour effectuer la division, on multiplie le numérateur et le dénominateur par le conjugué du dénominateur : z = -(2 - i)(1 - i) / (1 + i)(1 - i) = -(2 - 2i - i - 1) / (1 + 1) = -(1 - 3i) / 2 = -1/2 + (3/2)i.

Équations du Second Degré

Les équations du second degré en z ont la forme az² + bz + c = 0, où a, b, et c sont des nombres complexes et a ≠ 0. La méthode de résolution est similaire à celle des équations réelles, en utilisant le discriminant Δ = b² - 4ac.

• Si Δ = 0, l'équation a une solution unique : z = -b / 2a.
• Si Δ ≠ 0, on trouve les racines carrées complexes de Δ, notées δ, telles que δ² = Δ. Les solutions de l'équation sont alors : z₁ = (-b + δ) / 2a et z₂ = (-b - δ) / 2a.

Interprétation Géométrique

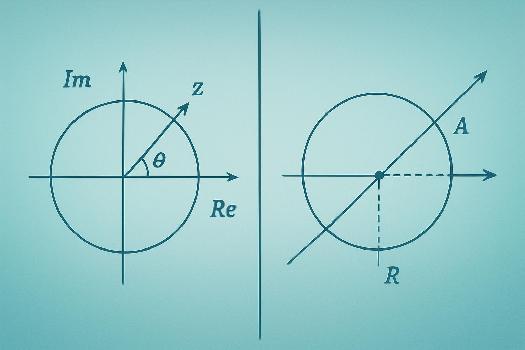
Chaque nombre complexe z = a + bi peut être représenté par un point M de coordonnées (a, b) dans le plan complexe. La résolution d'équations complexes peut être interprétée géométriquement. Par exemple, l'équation |z - z₀| = r représente l'ensemble des points M du plan complexe tels que la distance entre M et le point M₀ d'affixe z₀ est égale à r. C'est un cercle de centre M₀ et de rayon r. De même, l'équation arg(z - z₀) = θ représente l'ensemble des points M du plan complexe tels que l'angle entre la demi-droite [M₀M) et l'axe réel est égal à θ. C'est une demi-droite d'origine M₀ faisant un angle θ avec l'axe réel. La résolution d'équations complexes combinant module et argument permet de déterminer des lieux géométriques précis dans le plan complexe.

Exemple Avancé: Utilisation des Transformations Géométriques

Considérons l'équation z' = (z - 1) / (z + 1). On cherche l'ensemble des points M d'affixe z tels que z' soit un imaginaire pur. On peut écrire z = x + iy, où x et y sont des nombres réels. Alors, z' = (x + iy - 1) / (x + iy + 1) = ((x - 1) + iy) / ((x + 1) + iy). Pour que z' soit un imaginaire pur, sa partie réelle doit être nulle. On multiplie le numérateur et le dénominateur par le conjugué du dénominateur et on annule la partie réelle du résultat. Ceci conduit à une équation en x et y, qui représente un cercle privé d'un point.

Ce qu'il faut retenir

• Une équation complexe est une équation dont l'inconnue est un nombre complexe.
• Les équations du premier degré az + b = 0 se résolvent simplement par z = -b/a.
• Les équations du second degré az² + bz + c = 0 se résolvent à l'aide du discriminant Δ = b² - 4ac et des racines carrées de Δ.
• La résolution d'équations complexes peut être interprétée géométriquement dans le plan complexe (cercles, droites, demi-droites).
• Les transformations géométriques permettent de résoudre des équations complexes plus complexes et de déterminer des lieux géométriques.