Guide Complet des Dérivées de Fonctions Usuelles

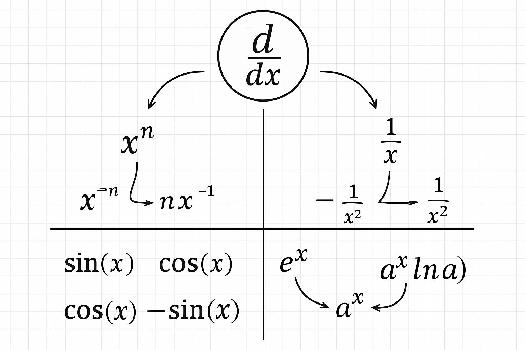
Dérivées des Fonctions Polynômes

Les fonctions polynômes sont des expressions de la forme f(x) = a_nxⁿ + a_n-1x^n-1 + ... + a₁x + a₀, où les a_i sont des coefficients constants et n est un entier non négatif. La dérivée d'une fonction polynôme se calcule terme par terme.

Règle de base: Si f(x) = xⁿ, alors f'(x) = nx^n-1. De plus, la dérivée d'une constante multipliée par une fonction est la constante multipliée par la dérivée de la fonction: si f(x) = k*g(x), alors f'(x) = k*g'(x).

Exemple 1: Soit f(x) = 3x² + 2x - 5. Alors f'(x) = 3 * 2x^2-1 + 2 * 1x^1-1 - 0 = 6x + 2.

Exemple 2: Soit g(x) = x⁴ - x³ + 7x. Alors g'(x) = 4x³ - 3x² + 7.

Dérivées des Fonctions Rationnelles

Une fonction rationnelle est une fonction de la forme f(x) = u(x) / v(x), où u(x) et v(x) sont des polynômes. Pour dériver une fonction rationnelle, on utilise la règle du quotient:

Règle du quotient: Si f(x) = u(x) / v(x), alors f'(x) = [u'(x)v(x) - u(x)v'(x)] / [v(x)]².

Exemple: Soit f(x) = (x² + 1) / (x - 2). Alors u(x) = x² + 1 et v(x) = x - 2. On a u'(x) = 2x et v'(x) = 1. Donc, f'(x) = [2x(x - 2) - (x² + 1)(1)] / (x - 2)² = (2x² - 4x - x² - 1) / (x - 2)² = (x² - 4x - 1) / (x - 2)².

Dérivées des Fonctions Trigonométriques

Les fonctions trigonométriques de base sont le sinus (sin), le cosinus (cos), la tangente (tan), etc. Il est essentiel de connaître leurs dérivées par cœur.

Dérivées principales:

• La dérivée de sin(x) est cos(x).
• La dérivée de cos(x) est -sin(x).
• La dérivée de tan(x) est 1 + tan²(x) = 1 / cos²(x).

Dérivées des Fonctions Exponentielles

Une fonction exponentielle est de la forme f(x) = a^x, où a est une constante positive. Le cas le plus courant est la fonction exponentielle naturelle e^x.

Dérivées principales:

• La dérivée de e^x est e^x.
• La dérivée de a^x est a^xln(a).

Dérivées des Fonctions Logarithmiques

Une fonction logarithmique est l'inverse d'une fonction exponentielle. Le cas le plus courant est le logarithme naturel, noté ln(x).

Dérivées principales:

• La dérivée de ln(x) est 1/x.
• La dérivée de log_a(x) est 1 / (xln(a)).

Ce qu'il faut retenir

• Fonctions Polynômes: (xⁿ)' = nx^n-1.
• Fonctions Rationnelles: Utilisez la règle du quotient.
• Fonctions Trigonométriques: Connaître les dérivées de sin(x), cos(x) et tan(x).
• Fonctions Exponentielles: (e^x)' = e^x et (a^x)' = a^xln(a).
• Fonctions Logarithmiques: (ln(x))' = 1/x.