Mathématiques > Analyse > Continuité > Continuité sur un intervalle

Prolongement par continuité

Apprenez à prolonger une fonction par continuité. Découvrez les conditions nécessaires, des exemples détaillés et la méthode à suivre pour étendre le domaine de définition d'une fonction tout en préservant sa continuité. Ressource destinée aux lycéens en mathématiques.

Définition du prolongement par continuité

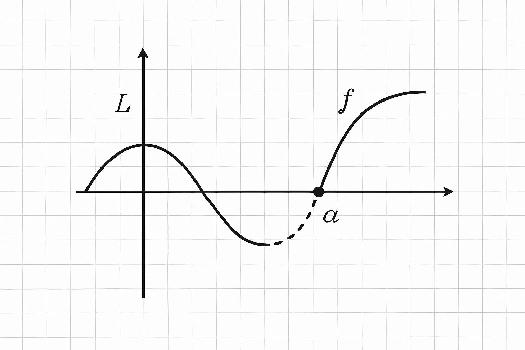
Soit f une fonction définie sur un intervalle I, sauf peut-être en un point a appartenant à I. On dit que f est prolongeable par continuité en a s'il existe une limite finie de f(x) lorsque x tend vers a.

Si limx→a f(x) = L (où L est un nombre réel), alors on peut définir une nouvelle fonction g de la manière suivante :

  • g(x) = f(x) pour tout x appartenant à I et différent de a.
  • g(a) = L

La fonction g est alors continue en a, et on dit qu'elle est le prolongement par continuité de f en a.

Conditions nécessaires pour un prolongement par continuité

Pour qu'une fonction f soit prolongeable par continuité en un point a, il est essentiel que la limite de f(x) lorsque x tend vers a existe et soit finie. C'est-à-dire :

  • limx→a f(x) = L, où L ∈ ℝ

Si cette limite n'existe pas (par exemple, si elle est infinie ou si les limites à gauche et à droite sont différentes), alors la fonction n'est pas prolongeable par continuité en a.

Exemples de prolongements par continuité

Voici quelques exemples illustrant le prolongement par continuité :

Exemple 1 :

Considérons la fonction f(x) = (sin(x)) / x, définie pour tout x ≠ 0.

Calculons la limite de f(x) lorsque x tend vers 0 :

limx→0 (sin(x)) / x = 1 (c'est une limite remarquable).

On peut donc prolonger f par continuité en 0 en définissant g(x) comme suit :

  • g(x) = (sin(x)) / x pour x ≠ 0
  • g(0) = 1

La fonction g est alors continue en 0.

Exemple 2 :

Considérons la fonction f(x) = (x2 - 4) / (x - 2), définie pour tout x ≠ 2.

On peut simplifier l'expression de f(x) :

f(x) = (x2 - 4) / (x - 2) = (x - 2)(x + 2) / (x - 2) = x + 2 (pour x ≠ 2)

Calculons la limite de f(x) lorsque x tend vers 2 :

limx→2 f(x) = limx→2 (x + 2) = 4

On peut donc prolonger f par continuité en 2 en définissant g(x) comme suit :

  • g(x) = (x2 - 4) / (x - 2) pour x ≠ 2
  • g(2) = 4

La fonction g est alors continue en 2.

Méthode pour prolonger une fonction par continuité

Voici une méthode générale pour prolonger une fonction par continuité en un point a :

  1. Vérifier si la fonction f est définie en a. Si elle l'est, il n'y a pas de prolongement à faire.
  2. Calculer la limite de f(x) lorsque x tend vers a. Si cette limite existe et est finie, notons-la L.
  3. Définir une nouvelle fonction g de la manière suivante :
    • g(x) = f(x) pour tout x ≠ a
    • g(a) = L
  4. Vérifier que la fonction g est bien continue en a. C'est-à-dire, vérifier que limx→a g(x) = g(a).

Ce qu'il faut retenir

  • Une fonction f est prolongeable par continuité en un point a si limx→a f(x) existe et est finie.
  • Si limx→a f(x) = L, on définit le prolongement par continuité g tel que g(x) = f(x) pour x ≠ a et g(a) = L.
  • Pour effectuer un prolongement par continuité, il est crucial de vérifier l'existence et la finitude de la limite.
  • Le prolongement par continuité permet de rendre une fonction continue en un point où elle ne l'était pas initialement.

← Primitives d'une fonction : Définition, calcul et exemples Propriété de positivité de l'intégrale →

FAQ

  • Peut-on prolonger une fonction par continuité si la limite est infinie ?

    Non, une fonction ne peut pas être prolongée par continuité si la limite en un point est infinie. Le prolongement par continuité nécessite une limite finie.
  • Que se passe-t-il si les limites à gauche et à droite en un point sont différentes ?

    Si les limites à gauche et à droite en un point sont différentes, la fonction n'est pas prolongeable par continuité en ce point, car la limite bilatérale n'existe pas.