Décomposition en facteurs premiers : Une exploration complète

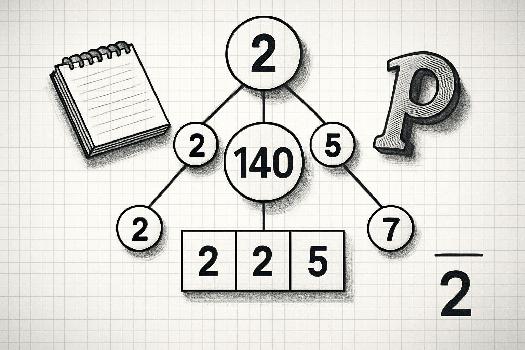
Introduction à la Décomposition en Facteurs Premiers

La décomposition en facteurs premiers est un concept fondamental en arithmétique. Elle consiste à exprimer un nombre entier comme un produit de nombres premiers. Comprendre cette décomposition est essentiel pour résoudre divers problèmes en mathématiques, notamment dans l'étude de la divisibilité et des congruences. Un nombre premier est un nombre entier supérieur à 1 qui n'a que deux diviseurs : 1 et lui-même. Les premiers nombres premiers sont 2, 3, 5, 7, 11, 13, 17, 19, etc. La décomposition en facteurs premiers permet de simplifier de nombreux calculs et de mieux comprendre la structure des nombres entiers.

Le Théorème Fondamental de l'Arithmétique

Le théorème fondamental de l'arithmétique stipule que tout entier supérieur à 1 peut être écrit comme un produit unique de nombres premiers, à l'ordre des facteurs près. Cette unicité est cruciale et rend la décomposition en facteurs premiers un outil puissant. En termes plus simples, cela signifie que pour n'importe quel nombre entier supérieur à 1, il existe une seule et unique façon de l'écrire comme un produit de nombres premiers. Par exemple, le nombre 12 peut être décomposé en 2 x 2 x 3 (ou 2² x 3). Il n'existe aucune autre façon de décomposer 12 en un produit de nombres premiers.

Méthode pour la Décomposition en Facteurs Premiers

Pour décomposer un nombre entier en facteurs premiers, on peut suivre les étapes suivantes :

1. Diviser par le plus petit nombre premier possible (2) : Si le nombre est pair, divisez-le par 2 autant de fois que possible jusqu'à ce qu'il devienne impair.
2. Diviser par le prochain nombre premier (3) : Si le nombre est divisible par 3, divisez-le par 3 autant de fois que possible.
3. Continuer avec les nombres premiers suivants (5, 7, 11, ...) : Répétez le processus avec les nombres premiers suivants jusqu'à ce que le quotient soit égal à 1.

1. 60 est divisible par 2 : 60 = 2 x 30
2. 30 est divisible par 2 : 30 = 2 x 15
3. 15 n'est pas divisible par 2, mais il est divisible par 3 : 15 = 3 x 5
4. 5 est un nombre premier.

Exemples de Décomposition en Facteurs Premiers

Voici quelques exemples supplémentaires pour illustrer la décomposition en facteurs premiers :

• 100 : 100 = 2 x 50 = 2 x 2 x 25 = 2 x 2 x 5 x 5 = 2² x 5²
• 84 : 84 = 2 x 42 = 2 x 2 x 21 = 2 x 2 x 3 x 7 = 2² x 3 x 7
• 147 : 147 = 3 x 49 = 3 x 7 x 7 = 3 x 7²

Applications de la Décomposition en Facteurs Premiers

La décomposition en facteurs premiers a de nombreuses applications en mathématiques et en informatique :

• Calcul du PGCD et du PPCM : La décomposition en facteurs premiers permet de calculer facilement le Plus Grand Commun Diviseur (PGCD) et le Plus Petit Commun Multiple (PPCM) de deux ou plusieurs nombres. Le PGCD est le produit des facteurs premiers communs aux deux nombres, élevés à la plus petite puissance. Le PPCM est le produit de tous les facteurs premiers présents dans les deux nombres, élevés à la plus grande puissance.
• Simplification de fractions : Elle permet de simplifier des fractions en divisant le numérateur et le dénominateur par leur PGCD.
• Cryptographie : La décomposition en facteurs premiers est à la base de certains algorithmes de cryptographie.
• Résolution d'équations diophantiennes : Elle peut être utilisée pour trouver les solutions entières d'équations.

Ce qu'il faut retenir

• Tout nombre entier supérieur à 1 peut être décomposé en un produit unique de nombres premiers.
• La décomposition en facteurs premiers est un outil fondamental en arithmétique.
• Pour décomposer un nombre en facteurs premiers, on le divise successivement par les nombres premiers (2, 3, 5, 7, ...).
• La décomposition en facteurs premiers permet de calculer le PGCD et le PPCM, de simplifier des fractions et est utilisée en cryptographie.