Mathématiques > Algèbre > Équations et Inéquations > Systèmes d'inéquations

Exercices Corrigés : Systèmes d'Inéquations Linéaires

Entraînez-vous à résoudre des systèmes d'inéquations linéaires avec cette série d'exercices corrigés, adaptés aux élèves de lycée. Chaque exercice est accompagné d'une solution détaillée, étape par étape.

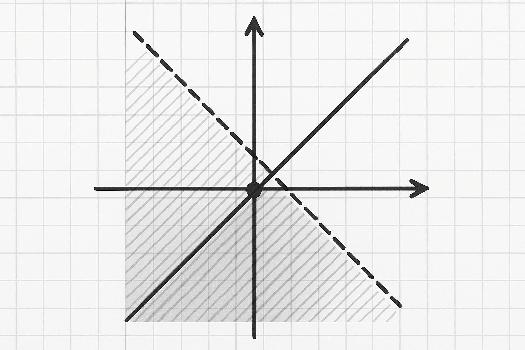
Exercice 1

Énoncé: Résolvez graphiquement le système d'inéquations suivant:

  • 2x + y ≥ 4
  • x - y ≤ 1
Solution:
  1. Tracer les droites: On trace les droites 2x + y = 4 et x - y = 1.
  2. Déterminer les régions solutions:
    • Pour 2x + y ≥ 4, on teste (0, 0): 2(0) + 0 ≥ 4 est faux. Donc, la région solution est le demi-plan ne contenant pas (0, 0).
    • Pour x - y ≤ 1, on teste (0, 0): 0 - 0 ≤ 1 est vrai. Donc, la région solution est le demi-plan contenant (0, 0).
  3. Identifier la région admissible: La région admissible est l'intersection des deux demi-plans, délimitée par les droites tracées. C'est la région où 2x + y ≥ 4 et x - y ≤ 1 sont simultanément vérifiées. (Un graphique illustrant la région admissible serait idéal ici)

Exercice 2

Énoncé: Déterminez la région admissible du système d'inéquations:

  • x ≥ 0
  • y ≥ 0
  • x + y ≤ 3
Solution:
  1. Interprétation des inéquations:
    • x ≥ 0 représente le demi-plan à droite de l'axe des y.
    • y ≥ 0 représente le demi-plan au-dessus de l'axe des x.
    • x + y ≤ 3 représente le demi-plan en dessous de la droite x + y = 3.
  2. Tracer la droite: On trace la droite x + y = 3.
  3. Déterminer la région solution: Pour x + y ≤ 3, on teste (0, 0): 0 + 0 ≤ 3 est vrai. Donc, la région solution est le demi-plan contenant (0, 0).
  4. Identifier la région admissible: La région admissible est l'intersection des trois régions, formant un triangle délimité par les axes x et y, et la droite x + y = 3. Les sommets du triangle sont (0, 0), (3, 0) et (0, 3). (Un graphique illustrant la région admissible serait idéal ici)

Exercice 3

Énoncé: Résolvez graphiquement le système d'inéquations suivant:

  • y > 2x - 1
  • y < -x + 4
Solution:
  1. Tracer les droites: On trace les droites y = 2x - 1 et y = -x + 4. Ces droites seront en pointillé car les inégalités sont strictes.
  2. Déterminer les régions solutions:
    • Pour y > 2x - 1, on teste (0, 0): 0 > 2(0) - 1 est vrai. Donc, la région solution est le demi-plan contenant (0, 0).
    • Pour y < -x + 4, on teste (0, 0): 0 < -0 + 4 est vrai. Donc, la région solution est le demi-plan contenant (0, 0).
  3. Identifier la région admissible: La région admissible est l'intersection des deux demi-plans, délimitée par les droites en pointillé. (Un graphique illustrant la région admissible serait idéal ici)

Ce qu'il faut retenir

  • Toujours tracer les droites associées aux inéquations.
  • Utiliser un point test pour déterminer le demi-plan solution de chaque inéquation.
  • La région admissible est l'intersection de toutes les régions solutions.
  • Faire attention aux inégalités strictes (< ou >), les droites sont tracées en pointillé.

← Exercices Corrigés : Détermination du Signe d'un Polynôme du Second Degré Exercices corrigés : Maîtriser le sens de variation et les extrema des fonctions →

FAQ

  • Que faire si la région admissible est vide?

    Si la région admissible est vide, cela signifie que le système d'inéquations n'a pas de solution. Il n'existe aucune valeur des variables qui puisse satisfaire toutes les inéquations simultanément.
  • Est-il possible d'avoir un système d'inéquations avec une seule solution?

    Théoriquement, oui, mais c'est très rare. Cela se produirait si la région admissible se réduisait à un seul point, ce qui impliquerait une configuration très spécifique des inéquations.