Résolution de Systèmes d'Équations Linéaires par Combinaison Linéaire (Élimination)

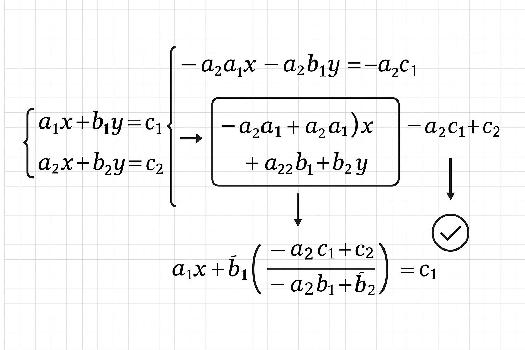
Introduction à la Méthode de Combinaison Linéaire

La méthode de combinaison linéaire, également connue sous le nom de méthode d'élimination, est une technique pour résoudre des systèmes d'équations linéaires. L'idée est d'éliminer une des variables en combinant les équations de manière appropriée. Cela conduit à une équation avec une seule variable, qu'il est facile de résoudre. Comme pour la substitution, le but est de trouver les valeurs des variables qui satisfont toutes les équations du système.

Étapes de la Méthode de Combinaison Linéaire

Voici les étapes détaillées pour la méthode de combinaison linéaire :

1. Multiplier les équations (si nécessaire): Multipliez une ou les deux équations par des constantes de manière à ce que les coefficients d'une des variables soient égaux ou opposés. Le but est de pouvoir annuler cette variable par addition ou soustraction.
2. Additionner ou soustraire les équations: Additionnez ou soustrayez les équations modifiées pour éliminer une des variables. Si les coefficients sont opposés, vous additionnez. S'ils sont égaux, vous soustrayez.
3. Résoudre l'équation résultante: Résolvez l'équation à une seule variable pour trouver sa valeur.
4. Substituer pour trouver l'autre variable: Remplacez la valeur que vous avez trouvée dans l'une des équations originales pour trouver la valeur de l'autre variable.
5. Vérifier: Vérifiez vos solutions en les substituant dans les équations originales.

Exemple 1: Élimination Directe

Considérons le système suivant: x + y = 5 x - y = 1

1. Les coefficients de 'y' sont opposés: Pas besoin de multiplier.
2. Additionner les équations: (x + y) + (x - y) = 5 + 1 => 2x = 6
3. Résoudre pour 'x': x = 3
4. Substituer 'x' dans la première équation: 3 + y = 5 => y = 2
5. Vérifier: 3 + 2 = 5 (Vrai) et 3 - 2 = 1 (Vrai). Donc, la solution est x = 3 et y = 2.

Exemple 2: Multiplication Nécessaire

Considérons le système suivant: 2x + y = 7 x + 3y = 4

1. Multiplier la deuxième équation par -2: -2(x + 3y) = -2(4) => -2x - 6y = -8
2. Additionner les équations: (2x + y) + (-2x - 6y) = 7 + (-8) => -5y = -1
3. Résoudre pour 'y': y = 1/5
4. Substituer 'y' dans la première équation: 2x + 1/5 = 7 => 2x = 34/5 => x = 17/5
5. Vérifier: 2(17/5) + 1/5 = 7 (Vrai) et 17/5 + 3(1/5) = 4 (Vrai). Donc, la solution est x = 17/5 et y = 1/5.

Cas Particuliers (Rappel)

Comme avec la substitution, la méthode de combinaison linéaire peut également révéler des cas particuliers :

• Aucune solution : Si l'élimination conduit à une contradiction (par exemple, 0 = 1), le système n'a pas de solution.
• Infinité de solutions : Si l'élimination conduit à une identité (par exemple, 0 = 0), le système a une infinité de solutions.

Ce qu'il faut retenir

• Méthode de combinaison linéaire (élimination) : Éliminer une variable en combinant les équations.
• Étapes clés : Multiplier (si nécessaire), additionner/soustraire, résoudre, substituer, vérifier.
• Objectif : Simplifier le système pour isoler une variable.
• Cas particuliers : Absence de solution (contradiction) ou infinité de solutions (identité).