Mathématiques > Algèbre > Fonctions > Parité et périodicité des fonctions

Fonctions Paires et Impaires : Comprendre et Identifier

Explorez en détail les concepts de parité et d'imparité des fonctions, avec des exemples concrets et des méthodes pour les identifier graphiquement et algébriquement. Conçu pour les élèves de lycée.

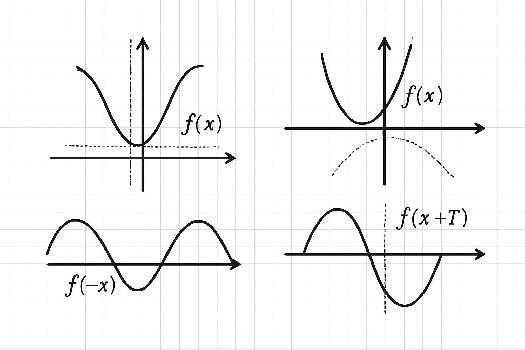
Définition d'une fonction paire

Une fonction f est dite paire si, pour tout x dans son domaine de définition, f(-x) = f(x). Cela signifie que la valeur de la fonction pour x est la même que pour -x.

  • Exemple: La fonction f(x) = x2 est une fonction paire. En effet, f(-x) = (-x)2 = x2 = f(x).
  • Interprétation graphique: Le graphique d'une fonction paire est symétrique par rapport à l'axe des ordonnées (axe des y). Si vous pliez le graphique le long de l'axe des y, les deux moitiés coïncident.

Définition d'une fonction impaire

Une fonction f est dite impaire si, pour tout x dans son domaine de définition, f(-x) = -f(x). Cela signifie que la valeur de la fonction pour -x est l'opposé de la valeur de la fonction pour x.

  • Exemple: La fonction f(x) = x3 est une fonction impaire. En effet, f(-x) = (-x)3 = -x3 = -f(x).
  • Interprétation graphique: Le graphique d'une fonction impaire est symétrique par rapport à l'origine. Si vous effectuez une rotation de 180° autour de l'origine, le graphique reste inchangé.

Méthode algébrique pour déterminer la parité d'une fonction

Pour déterminer algébriquement si une fonction est paire, impaire, ou ni l'un ni l'autre, suivez ces étapes :

  1. Remplacez x par -x dans l'expression de la fonction f(x).
  2. Simplifiez l'expression f(-x).
  3. Comparez f(-x) avec f(x) :
    • Si f(-x) = f(x), alors la fonction est paire.
    • Si f(-x) = -f(x), alors la fonction est impaire.
    • Si f(-x) n'est ni égal à f(x) ni à -f(x), alors la fonction n'est ni paire ni impaire.
Exemple : Soit f(x) = x4 + 2x2 + 1. Alors f(-x) = (-x)4 + 2(-x)2 + 1 = x4 + 2x2 + 1 = f(x). Donc, la fonction est paire.

Méthode graphique pour déterminer la parité d'une fonction

L'observation du graphique permet de déterminer rapidement la parité :

  • Fonction paire : Si le graphique est symétrique par rapport à l'axe des ordonnées, la fonction est paire.
  • Fonction impaire : Si le graphique est symétrique par rapport à l'origine, la fonction est impaire.
  • Fonction ni paire ni impaire : Si le graphique ne présente aucune de ces symétries, la fonction n'est ni paire ni impaire.

Exemples de fonctions paires, impaires et ni l'un ni l'autre

  • Fonctions paires :f(x) = x2, f(x) = cos(x), f(x) = |x| (valeur absolue de x).
  • Fonctions impaires :f(x) = x3, f(x) = sin(x), f(x) = x.
  • Fonctions ni paires ni impaires :f(x) = x2 + x, f(x) = ex, f(x) = x + 1.

Périodicité d'une fonction

Une fonction f est dite périodique de période T (où T est un nombre réel non nul) si, pour tout x dans son domaine de définition, f(x + T) = f(x). La plus petite valeur positive de T pour laquelle cette égalité est vraie est appelée la période fondamentale de la fonction.

  • Exemple : La fonction f(x) = sin(x) est périodique de période 2π. En effet, sin(x + 2π) = sin(x) pour tout x.
  • Interprétation graphique : Le graphique d'une fonction périodique se répète à intervalles réguliers. La distance entre deux points consécutifs où le graphique se répète est la période.

Déterminer la périodicité d'une fonction

Pour déterminer si une fonction est périodique, on peut essayer de trouver une valeur T telle que f(x + T) = f(x) pour tout x. Pour certaines fonctions, comme les fonctions trigonométriques, la périodicité est évidente. Pour d'autres, il peut être nécessaire d'utiliser des identités trigonométriques ou d'autres techniques algébriques. L'observation du graphique est aussi un bon moyen de déterminer la période.

Exemples de fonctions périodiques et non périodiques

  • Fonctions périodiques :f(x) = sin(x), f(x) = cos(x), f(x) = tan(x).
  • Fonctions non périodiques :f(x) = x, f(x) = x2, f(x) = ex.

Ce qu'il faut retenir

  • Fonction paire : f(-x) = f(x). Symétrie par rapport à l'axe des ordonnées.
  • Fonction impaire : f(-x) = -f(x). Symétrie par rapport à l'origine.
  • Fonction périodique : f(x + T) = f(x), où T est la période. Le graphique se répète à intervalles réguliers.
  • Pour déterminer algébriquement la parité, substituer -x à x et simplifier.
  • Graphiquement, observer les symétries.

← Fonctions Linéaires et Proportionnalité Forme canonique d'une fonction quadratique →

FAQ

  • Une fonction peut-elle être à la fois paire et impaire ?

    Oui, mais seulement si cette fonction est la fonction nulle, c'est-à-dire f(x) = 0 pour tout x. En effet, f(-x) = 0 = f(x) et f(-x) = 0 = -f(x).
  • Comment reconnaître graphiquement une fonction périodique ?

    Le graphique d'une fonction périodique se répète à intervalles réguliers. Vous pouvez identifier la période en mesurant la distance horizontale entre deux points consécutifs où le motif se répète.
  • Toutes les fonctions sont-elles paires, impaires ou périodiques ?

    Non, la plupart des fonctions ne sont ni paires, ni impaires, ni périodiques. Il existe des fonctions sans aucune symétrie particulière ni répétition.