Introduction intuitive à la continuité d'une fonction

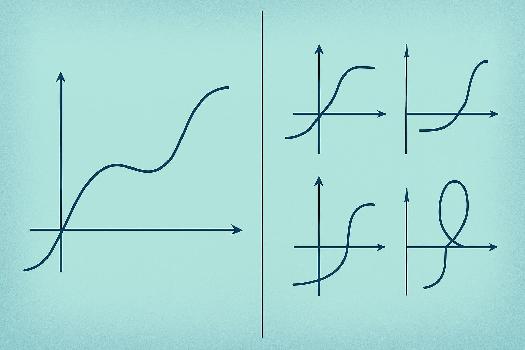
Qu'est-ce que la continuité ? Une approche visuelle

La continuité d'une fonction peut être comprise intuitivement comme la possibilité de tracer le graphe de la fonction sans lever le crayon. En d'autres termes, il n'y a pas de 'saut' ou de 'trou' dans le graphe.

Exemple concret : Imaginez une route sans interruption. Vous pouvez la parcourir en continu. Une fonction continue est similaire : on peut suivre son graphe sans interruption.

Identifier les discontinuités

Une discontinuité se produit lorsqu'il y a un 'saut', un 'trou' ou un 'point isolé' dans le graphe de la fonction. Examinons quelques exemples :

1. Saut : Imaginez une fonction qui passe brusquement d'une valeur à une autre. Il y a un saut à cet endroit.
2. Trou : Il peut y avoir un point manquant dans le graphe. Par exemple, la fonction est définie partout sauf en un point précis.
3. Point isolé : Un point isolé est un point qui n'est pas 'connecté' au reste du graphe. Il existe une valeur isolée pour un 'x' particulier.

Exemple : La fonction f(x) = 1/x est discontinue en x=0 car elle tend vers l'infini quand x approche 0. On ne peut pas tracer le graphe sans lever le crayon.

Continuité en un point

Pour qu'une fonction soit continue en un point 'a', trois conditions doivent être remplies :

1. La fonction doit être définie en 'a' : f(a) doit exister.
2. La limite de f(x) quand x tend vers 'a' doit exister : lim (x→a) f(x) doit avoir une valeur.
3. La limite doit être égale à la valeur de la fonction en 'a' : lim (x→a) f(x) = f(a).

Si l'une de ces conditions n'est pas remplie, la fonction est discontinue en 'a'.

Exemples de fonctions continues

Voici quelques exemples courants de fonctions continues :

1. Fonctions polynomiales : f(x) = x² + 3x - 1, f(x) = 5x³ + 2x + 7, etc. Ces fonctions sont continues sur tout l'ensemble des nombres réels.
2. Fonctions exponentielles : f(x) = e^x, f(x) = 2^x, etc. Elles sont également continues sur tout l'ensemble des nombres réels.
3. Fonctions trigonométriques : sin(x), cos(x). Elles sont continues sur tout l'ensemble des nombres réels.

Les fonctions rationnelles (un polynôme divisé par un autre) sont continues partout sauf aux points où le dénominateur est égal à zéro.

Continuité sur un intervalle

Une fonction est dite continue sur un intervalle si elle est continue en chaque point de cet intervalle.

Exemple: La fonction f(x) = x² est continue sur l'intervalle [0, 5] car elle est continue en chaque point entre 0 et 5 (inclus).

Applications de la continuité

La continuité est une notion fondamentale en mathématiques et a de nombreuses applications :

1. Calcul de limites : Si une fonction est continue en un point, le calcul de la limite est simple : il suffit d'évaluer la fonction en ce point.
2. Théorème des valeurs intermédiaires (TVI) : Si une fonction est continue sur un intervalle [a, b], alors elle prend toutes les valeurs entre f(a) et f(b). Ce théorème est utilisé pour prouver l'existence de solutions à certaines équations.
3. Optimisation : La continuité est une condition nécessaire pour l'existence d'un maximum ou d'un minimum sur un intervalle fermé.

Ce qu'il faut retenir

• Définition intuitive : On peut tracer le graphe de la fonction sans lever le crayon.
• Discontinuités : Sauts, trous, points isolés.
• Continuité en un point 'a' : f(a) existe, lim (x→a) f(x) existe, lim (x→a) f(x) = f(a).
• Exemples de fonctions continues : Fonctions polynomiales, exponentielles, trigonométriques (sin(x) et cos(x)).
• Applications : Calcul de limites, Théorème des valeurs intermédiaires, Optimisation.