Introduction intuitive aux limites de fonctions

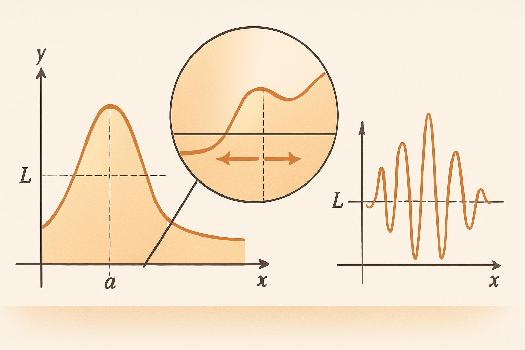
Qu'est-ce qu'une limite ? Une première approche

Imaginez une fourmi qui se rapproche d'un morceau de sucre. Elle se rapproche de plus en plus, mais sans jamais l'atteindre complètement. La limite d'une fonction, c'est un peu la même idée. On regarde ce vers quoi la fonction se rapproche quand la variable s'approche d'une certaine valeur (sans forcément l'atteindre).

Prenons un exemple simple: la fonction f(x) = x + 1. Si x se rapproche de 2 (par exemple, en prenant les valeurs 1.9, 1.99, 1.999...), alors f(x) se rapproche de 3 (2.9, 2.99, 2.999...). On dit que la limite de f(x) quand x tend vers 2 est 3, et on note cela: lim _x→2 f(x) = 3.

Se rapprocher... de plus en plus près!

La clé de la notion de limite, c'est de se rapprocher indéfiniment. Ce n'est pas suffisant de juste s'approcher un peu. On doit pouvoir s'approcher aussi près que l'on veut. Reprenons notre fourmi. Peu importe à quelle distance du sucre je la place, elle doit pouvoir se rapprocher de moitié, puis de moitié encore, et encore... sans jamais s'arrêter.

Mathématiquement, ça veut dire que si je veux que f(x) soit à moins de 0.0001 de 3, je dois pouvoir trouver des valeurs de x suffisamment proches de 2 pour que ça arrive. Et si je veux que f(x) soit à moins de 0.000000001 de 3, je dois encore pouvoir trouver de tels x. Si c'est possible, alors la limite existe et vaut 3.

Cas où la limite n'existe pas

Toutes les fonctions n'ont pas de limite en tous les points. Il existe plusieurs situations où la limite n'existe pas:

1. Sauts: Imaginez une fonction qui vaut 1 pour x < 0 et 2 pour x ≥ 0. Quand x s'approche de 0 par la gauche, f(x) se rapproche de 1. Mais quand x s'approche de 0 par la droite, f(x) se rapproche de 2. Comme les deux "côtés" ne se rejoignent pas, la limite en 0 n'existe pas.

2. Oscillations infinies: Considérez la fonction f(x) = sin(1/x). Quand x s'approche de 0, la fonction oscille de plus en plus vite entre -1 et 1. Elle ne se stabilise vers aucune valeur en particulier, donc la limite en 0 n'existe pas.

3. Tend vers l'infini: Si f(x) devient de plus en plus grand (positivement ou négativement) quand x s'approche d'une certaine valeur, on dit que la limite est l'infini (ou moins l'infini). Techniquement, la limite n'existe toujours pas (car l'infini n'est pas un nombre), mais on utilise cette notation pour décrire le comportement de la fonction.

Exemples concrets

Voici quelques exemples pour illustrer la notion de limite:

1. f(x) = x². lim _x→3 f(x) = 9. Quand x se rapproche de 3, x² se rapproche de 9.

2. f(x) = (x² - 1) / (x - 1). Cette fonction n'est pas définie en x = 1. Cependant, si x s'approche de 1, f(x) se rapproche de 2. On peut le voir en simplifiant l'expression: f(x) = (x + 1)(x - 1) / (x - 1) = x + 1 (pour x ≠ 1). Donc lim _x→1 f(x) = 2.

3. f(x) = 1/x. lim _x→∞ f(x) = 0. Quand x devient très grand, 1/x se rapproche de 0.

Limites à gauche et à droite

Parfois, il est important de considérer si on s'approche d'une valeur par la gauche (valeurs plus petites) ou par la droite (valeurs plus grandes). On parle alors de limite à gauche et de limite à droite.

On note lim _x→a^- f(x) la limite à gauche de f(x) quand x tend vers a, et lim _x→a⁺ f(x) la limite à droite.

Pour qu'une limite (ordinaire) existe, il faut et il suffit que la limite à gauche et la limite à droite existent et soient égales.

Ce qu'il faut retenir

• La limite d'une fonction en un point est la valeur vers laquelle la fonction se rapproche quand la variable se rapproche de ce point.
• Il faut se rapprocher indéfiniment de cette valeur.
• La limite n'existe pas toujours (sauts, oscillations, infini).
• Il faut considérer les limites à gauche et à droite. Si elles sont différentes, la limite n'existe pas.
• La notation est : lim _x→a f(x) = L