Forme Trigonométrique d'un Nombre Complexe

Introduction à la Forme Trigonométrique

Un nombre complexe z peut être représenté de différentes manières. Nous connaissons déjà la forme algébrique z = a + ib, où a est la partie réelle et b la partie imaginaire. La forme trigonométrique offre une perspective géométrique et est particulièrement utile pour certaines opérations, comme les multiplications et les divisions.

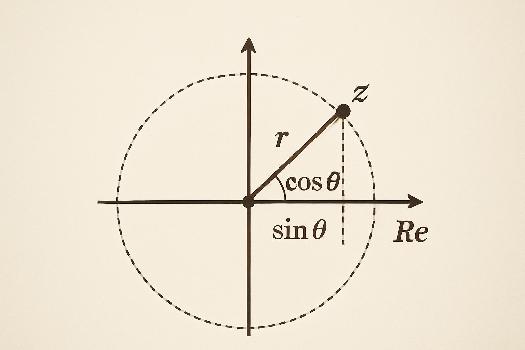
L'idée principale est d'exprimer un nombre complexe en utilisant son module (la distance à l'origine) et son argument (l'angle avec l'axe réel positif).

Module d'un Nombre Complexe

Le module d'un nombre complexe z = a + ib, noté |z|, est défini comme la distance de z à l'origine dans le plan complexe. Il est calculé par la formule :

|z| = √(a² + b²)

Exemple : Si z = 3 + 4i, alors |z| = √(3² + 4²) = √(9 + 16) = √25 = 5.

Le module est toujours un nombre réel positif ou nul.

Argument d'un Nombre Complexe

L'argument d'un nombre complexe non nul z, noté arg(z), est l'angle (en radians) entre l'axe réel positif et la droite reliant l'origine à z dans le plan complexe. Il est défini à 2π près, c'est-à-dire que arg(z) et arg(z) + 2π représentent le même argument.

Si z = a + ib, on peut trouver un argument θ de z en utilisant les relations suivantes :

cos(θ) = a / |z| et sin(θ) = b / |z|

Attention : Il est important de déterminer le quadrant dans lequel se trouve z pour choisir la bonne valeur de θ.

Exemple : Si z = 1 + i, alors |z| = √2. Donc, cos(θ) = 1/√2 et sin(θ) = 1/√2. Cela signifie que θ = π/4 (modulo 2π).

Forme Trigonométrique

Si z est un nombre complexe de module |z| = r et d'argument arg(z) = θ, alors la forme trigonométrique de z est donnée par :

z = r(cos(θ) + i sin(θ))

Exemple : Reprenons z = 1 + i. Nous avons |z| = √2 et θ = π/4. Donc, la forme trigonométrique de z est :

z = √2 (cos(π/4) + i sin(π/4))

Passage de la Forme Algébrique à la Forme Trigonométrique

1. Calculer le module |z| = √(a² + b²).
2. Trouver un argument θ en utilisant les équations cos(θ) = a / |z| et sin(θ) = b / |z|. Déterminer le quadrant de z pour choisir la bonne valeur de θ.
3. Écrire la forme trigonométrique z = |z|(cos(θ) + i sin(θ)).

Exemple : Soit z = -1 + i√3.

1. |z| = √((-1)² + (√3)²) = √(1 + 3) = √4 = 2.
2. cos(θ) = -1/2 et sin(θ) = √3/2. Puisque le cosinus est négatif et le sinus est positif, z est dans le deuxième quadrant. Donc, θ = 2π/3.
3. La forme trigonométrique est z = 2(cos(2π/3) + i sin(2π/3)).

Opérations avec la Forme Trigonométrique

• Multiplication : Si z₁ = r₁(cos(θ₁) + i sin(θ₁)) et z₂ = r₂(cos(θ₂) + i sin(θ₂)), alors z₁ * z₂ = r₁r₂(cos(θ₁ + θ₂) + i sin(θ₁ + θ₂)). Les modules sont multipliés et les arguments sont additionnés.
• Division : Si z₁ = r₁(cos(θ₁) + i sin(θ₁)) et z₂ = r₂(cos(θ₂) + i sin(θ₂)), alors z₁ / z₂ = (r₁/r₂)(cos(θ₁ - θ₂) + i sin(θ₁ - θ₂)). Les modules sont divisés et les arguments sont soustraits.

Ces règles simplifient grandement les calculs impliquant des nombres complexes.

Ce qu'il faut retenir

• La forme trigonométrique d'un nombre complexe z est z = r(cos(θ) + i sin(θ)), où r est le module de z et θ est son argument.
• Le module de z = a + ib est |z| = √(a² + b²).
• L'argument de z est l'angle θ tel que cos(θ) = a / |z| et sin(θ) = b / |z|. Il est défini à 2π près.
• Pour passer de la forme algébrique à la forme trigonométrique, calculez le module et trouvez un argument.
• La forme trigonométrique simplifie les multiplications et divisions de nombres complexes : les modules se multiplient/divisent et les arguments s'additionnent/soustraient.