Mathématiques > Graphes (Terminale - Spécialité) > Parcours et Algorithmes > Connexité

Algorithme d'identification des composantes connexes d'un graphe

Découvrez un algorithme simple et efficace pour identifier les composantes connexes d'un graphe, étape par étape, avec un exemple détaillé.

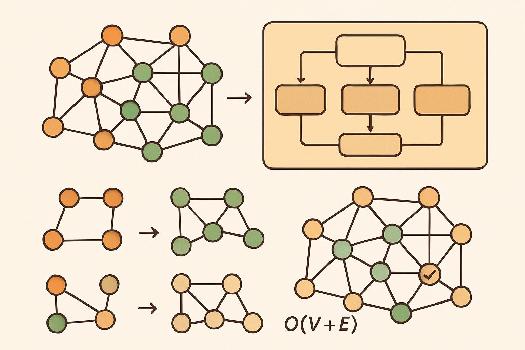
Présentation de l'algorithme

Cet algorithme a pour objectif de déterminer les différentes composantes connexes d'un graphe donné. Il utilise un parcours en profondeur (DFS) ou en largeur (BFS) pour explorer le graphe et identifier les ensembles de sommets connectés entre eux.

Étapes de l'algorithme

  1. Initialisation: Marquer tous les sommets comme non visités.
  2. Boucle principale: Parcourir tous les sommets du graphe.
  3. Vérification: Pour chaque sommet non visité, effectuer un parcours (DFS ou BFS) à partir de ce sommet.
  4. Identification de la composante connexe: Tous les sommets visités lors de ce parcours appartiennent à la même composante connexe.
  5. Marquage: Marquer tous les sommets de la composante connexe comme visités.
  6. Répétition: Répéter les étapes 2 à 5 jusqu'à ce que tous les sommets aient été visités.

Exemple détaillé

Considérons le graphe suivant (représenté par une liste d'adjacence):

  • A: [B, C]
  • B: [A, D]
  • C: [A]
  • D: [B]
  • E: [F]
  • F: [E]
  • G: []

Appliquons l'algorithme:
  1. Initialisation: Tous les sommets (A, B, C, D, E, F, G) sont marqués comme non visités.
  2. Boucle principale:
    • Sommet A: Non visité. On effectue un DFS à partir de A. On visite A, B, C, D. La composante connexe est {A, B, C, D}. On marque A, B, C, D comme visités.
    • Sommet E: Non visité. On effectue un DFS à partir de E. On visite E, F. La composante connexe est {E, F}. On marque E, F comme visités.
    • Sommet G: Non visité. On effectue un DFS à partir de G. On visite G. La composante connexe est {G}. On marque G comme visité.

Résultat: Le graphe a trois composantes connexes: {A, B, C, D}, {E, F}, et {G}.

Choix entre DFS et BFS

On peut utiliser soit le parcours en profondeur (DFS), soit le parcours en largeur (BFS) pour implémenter l'algorithme. Les deux méthodes sont valables. En général, le DFS est plus simple à implémenter de manière récursive, tandis que le BFS est plus adapté pour trouver le chemin le plus court entre deux sommets.

Complexité de l'algorithme

La complexité de l'algorithme est O(V + E), où V est le nombre de sommets et E est le nombre d'arêtes du graphe. Cela est dû au fait que chaque sommet et chaque arête sont visités au plus une fois lors du parcours (DFS ou BFS).

Ce qu'il faut retenir

  • Objectif : Identifier les composantes connexes d'un graphe.
  • Étapes : Initialisation, boucle principale, parcours (DFS ou BFS), identification de la composante connexe, marquage, répétition.
  • Exemple : Illustration de l'algorithme sur un graphe.
  • Complexité : O(V + E).

← Algorithmes de Parcours en Largeur (BFS) et Profondeur (DFS) →

FAQ

  • L'algorithme fonctionne-t-il pour les graphes orientés ?

    Non, cet algorithme identifie les composantes connexes, pas les composantes fortement connexes. Pour les graphes orientés, on utilise des algorithmes différents pour trouver les composantes fortement connexes.
  • Est-ce que l'ordre de parcours des sommets affecte le résultat de l'algorithme ?

    Non, l'ordre de parcours des sommets n'affecte pas le résultat final, c'est-à-dire les composantes connexes identifiées. Cependant, l'ordre dans lequel les sommets sont visités au sein d'une même composante peut varier en fonction de l'ordre initial.