Introduction au Produit Scalaire dans l'Espace

Définition et Interprétation Géométrique

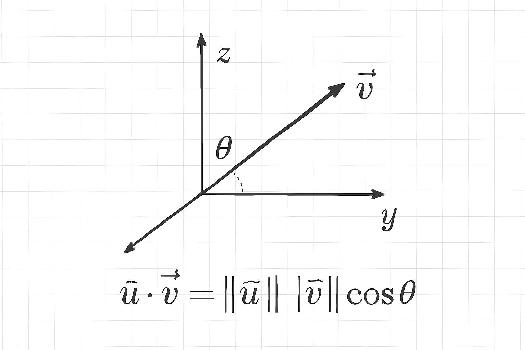
Le produit scalaire de deux vecteurs u et v dans l'espace, noté u · v, est un nombre réel. Il peut être défini de deux manières équivalentes:

1. Définition géométrique: u · v = ||u|| ||v|| cos(θ), où ||u|| et ||v|| sont les normes (longueurs) des vecteurs u et v, et θ est l'angle entre eux. Si l'un des vecteurs est nul, alors u · v = 0.

2. Définition analytique: Si u = (x₁, y₁, z₁) et v = (x₂, y₂, z₂), alors u · v = x₁x₂ + y₁y₂ + z₁z₂.

Interprétation géométrique: Le produit scalaire est lié à la projection d'un vecteur sur un autre. Si u · v > 0, l'angle entre u et v est aigu. Si u · v < 0, l'angle est obtus. Si u · v = 0, les vecteurs sont orthogonaux (perpendiculaires).

Propriétés du Produit Scalaire

Le produit scalaire possède plusieurs propriétés importantes, utiles pour les calculs et les démonstrations:

• Commutativité: u · v = v · u
• Distributivité par rapport à l'addition vectorielle: u · (v + w) = u · v + u · w
• Associativité par rapport à la multiplication scalaire: (ku) · v = k(u · v) = u · (kv), où k est un scalaire.
• Produit scalaire d'un vecteur avec lui-même: u · u = ||u||², ce qui est toujours positif ou nul.

Applications du Produit Scalaire

Le produit scalaire a de nombreuses applications en géométrie spatiale:

1. Calcul de l'angle entre deux vecteurs: cos(θ) = (u · v) / (||u|| ||v||)
2. Test d'orthogonalité: Deux vecteurs u et v sont orthogonaux si et seulement si u · v = 0.
3. Calcul de la projection d'un vecteur sur un autre: La projection de u sur v est (u · v / ||v||²) * v
4. Détermination d'équations de plans et de droites: Le produit scalaire permet de trouver des vecteurs normaux à un plan ou des vecteurs directeurs d'une droite.
5. Calcul de distances: Utile dans de nombreux problèmes géométriques faisant intervenir des distances.

Exemples Concrets

Exemple 1: Soient u = (1, 2, 3) et v = (4, 5, 6). Calculer u · v.
Solution: u · v = (1)(4) + (2)(5) + (3)(6) = 4 + 10 + 18 = 32.

Exemple 2: Déterminer si les vecteurs u = (2, -1, 3) et v = (1, 5, 1) sont orthogonaux.
Solution: u · v = (2)(1) + (-1)(5) + (3)(1) = 2 - 5 + 3 = 0. Donc, les vecteurs sont orthogonaux.

Exemple 3: Calculer l'angle entre les vecteurs u = (1, 0, 0) et v = (1, 1, 0).
Solution: ||u|| = 1, ||v|| = √2. u · v = 1. cos(θ) = 1 / (1 * √2) = 1/√2. Donc, θ = π/4 (45 degrés).

Ce qu'il faut retenir

• Définition: u · v = ||u|| ||v|| cos(θ) = x₁x₂ + y₁y₂ + z₁z₂.
• Orthogonalité: u · v = 0 si et seulement si u et v sont orthogonaux.
• Angle entre deux vecteurs: cos(θ) = (u · v) / (||u|| ||v||).
• Propriétés: Commutativité, distributivité, associativité.