Mathématiques > Analyse > Dérivation > Sens de variation d'une fonction et signe de la dérivée

Exercices corrigés : Sens de variation d'une fonction et signe de sa dérivée

Entrainez-vous avec des exercices corrigés détaillés sur la relation entre le sens de variation d'une fonction et le signe de sa dérivée. Appliquez les concepts théoriques à des problèmes concrets pour consolider votre compréhension et améliorer vos compétences en analyse. Idéal pour la préparation aux examens et concours.

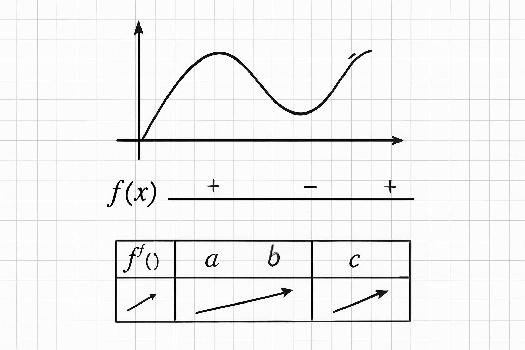
Exercice 1

Soit la fonction f(x) = x3 - 6x2 + 9x + 2. Déterminer son sens de variation et ses extrema locaux.

Correction de l'exercice 1

  1. Calcul de la dérivée : f'(x) = 3x2 - 12x + 9
  2. Points critiques : f'(x) = 0 => 3x2 - 12x + 9 = 0 => x2 - 4x + 3 = 0 => (x-1)(x-3) = 0 => x = 1 ou x = 3
  3. Tableau de signes de f'(x) :
    x-∞13+∞
    f'(x)+0-0+
  4. Tableau de variations de f(x) :
    x-∞13+∞
    f'(x)+0-0+
    f(x)croissanteMaximumdécroissanteMinimumcroissante
    La fonction est croissante sur ]-∞ ; 1] et [3 ; +∞[ et décroissante sur [1 ; 3]. Elle admet un maximum local en x = 1, qui vaut f(1) = 6, et un minimum local en x = 3, qui vaut f(3) = 2.

Exercice 2

Soit la fonction f(x) = (x2 + 1) / x. Déterminer son sens de variation et ses extrema locaux.

Correction de l'exercice 2

  1. Calcul de la dérivée : f(x) = x + 1/x donc f'(x) = 1 - 1/x2 = (x2 - 1) / x2
  2. Points critiques : f'(x) = 0 => x2 - 1 = 0 => x = -1 ou x = 1. De plus, f'(x) n'est pas définie en x=0, mais f(x) non plus.
  3. Tableau de signes de f'(x) :
    x-∞-101+∞
    x2-1+0--0+
    x2++0++
    f'(x)+0-||-0+
  4. Tableau de variations de f(x) :
    x-∞-101+∞
    f'(x)+0-||-0+
    f(x)croissanteMaximumdécroissante||décroissanteMinimumcroissante
    La fonction est croissante sur ]-∞ ; -1] et [1 ; +∞[ et décroissante sur [-1 ; 0[ et ]0 ; 1]. Elle admet un maximum local en x = -1, qui vaut f(-1) = -2, et un minimum local en x = 1, qui vaut f(1) = 2.

Ce qu'il faut retenir

  • Les exercices corrigés sont essentiels pour consolider la compréhension et appliquer les concepts théoriques.
  • La méthode de résolution reste la même : calculer la dérivée, trouver les points critiques, établir le tableau de signes et en déduire le tableau de variations.
  • Attention aux points où la dérivée n'est pas définie, ils peuvent aussi influencer le sens de variation.

← Exercices corrigés : Nombre dérivé et tangente Extrema Locaux et Globaux d'une Fonction : Définitions et Méthodes →

FAQ

  • Que faire si je n'arrive pas à factoriser la dérivée pour trouver les points critiques ?

    Utilisez des méthodes numériques (calculatrice, logiciel) pour trouver les racines de l'équation f'(x) = 0. Si la dérivée est un polynôme de degré 2, vous pouvez utiliser la formule du discriminant (Δ = b2 - 4ac) pour trouver les racines.
  • Comment interpréter un tableau de variations ?

    Le tableau de variations résume le comportement de la fonction. Les flèches indiquent si la fonction croît (flèche montante) ou décroît (flèche descendante). Les valeurs aux points critiques indiquent les maximums et minimums locaux. Les limites aux bornes de l'intervalle d'étude donnent une idée du comportement asymptotique de la fonction.