Mathématiques > Nombres Complexes (Terminale) > Introduction aux Nombres Complexes > Définition et notation (forme algébrique)

Introduction aux Nombres Complexes: Définition et Forme Algébrique

Découvrez les bases des nombres complexes, leur définition, leur notation sous forme algébrique, et comment les manipuler. Ce guide complet est parfait pour les élèves de Terminale.

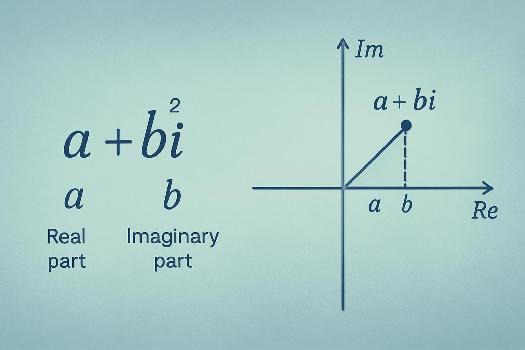
Définition d'un Nombre Complexe

Un nombre complexe est un nombre qui peut s'écrire sous la forme a + bi, où a et b sont des nombres réels, et i est l'unité imaginaire, définie par la propriété i² = -1.

  • a est appelée la partie réelle du nombre complexe, notée Re(z).
  • b est appelée la partie imaginaire du nombre complexe, notée Im(z).
L'ensemble des nombres complexes est noté ℂ.

Forme Algébrique d'un Nombre Complexe

La forme a + bi est appelée la forme algébrique du nombre complexe. Cette forme est unique pour chaque nombre complexe. Comprendre cette forme est crucial pour effectuer des opérations sur les nombres complexes.

Exemples:

  • 3 + 2i est un nombre complexe de partie réelle 3 et de partie imaginaire 2.
  • -1 - i est un nombre complexe de partie réelle -1 et de partie imaginaire -1.
  • 5i est un nombre complexe de partie réelle 0 et de partie imaginaire 5.
  • 7 est un nombre complexe de partie réelle 7 et de partie imaginaire 0 (un nombre réel est donc aussi un nombre complexe).

Notation des Nombres Complexes

Un nombre complexe est généralement noté z. On écrit alors z = a + bi. L'ensemble des nombres complexes, noté ℂ, contient tous les nombres de cette forme. Il est important de se rappeler que a et b sont des nombres réels, donc ils appartiennent à l'ensemble ℝ.

La notation z = a + bi facilite les opérations algébriques sur les nombres complexes.

L'importance de i² = -1

La définition i² = -1 est fondamentale. Elle permet de manipuler les expressions contenant i comme des expressions algébriques ordinaires, en gardant à l'esprit que i² peut être remplacé par -1.

Exemple:

  • (2i)² = 2² * i² = 4 * (-1) = -4

Représentation Graphique des Nombres Complexes

Un nombre complexe z = a + bi peut être représenté graphiquement dans le plan complexe. L'axe horizontal représente la partie réelle (Re(z) = a), et l'axe vertical représente la partie imaginaire (Im(z) = b). Le nombre complexe z est alors représenté par le point de coordonnées (a, b).

Cette représentation visuelle aide à comprendre les propriétés géométriques des nombres complexes.

Egalité de deux nombres complexes

Deux nombres complexes z = a + bi et z' = a' + b'i sont égaux si et seulement si leurs parties réelles et imaginaires sont égales, c'est-à-dire : a = a' et b = b'. Cette propriété est essentielle pour résoudre des équations impliquant des nombres complexes.

Exemple: Si x + yi = 3 - 2i, alors x = 3 et y = -2.

Ce qu'il faut retenir

  • Un nombre complexe est de la forme a + bi, où a et b sont réels et i² = -1.
  • a est la partie réelle et b la partie imaginaire.
  • La forme a + bi est la forme algébrique.
  • L'ensemble des nombres complexes est noté ℂ.
  • Les nombres complexes sont représentés dans le plan complexe par leurs coordonnées (a, b).
  • Deux nombres complexes sont égaux si et seulement si leurs parties réelles et imaginaires sont égales.

← Interprétation Géométrique des Nombres Complexes : Affixe et Point Image Opérations sur les Nombres Complexes →

FAQ

  • Qu'est-ce que l'unité imaginaire i ?

    L'unité imaginaire i est définie comme la racine carrée de -1, c'est-à-dire i² = -1.
  • Un nombre réel est-il un nombre complexe ?

    Oui, un nombre réel a peut être considéré comme un nombre complexe de la forme a + 0i. Sa partie imaginaire est nulle.
  • Comment identifier la partie réelle et la partie imaginaire d'un nombre complexe ?

    Dans un nombre complexe de la forme a + bi, a est la partie réelle et b est la partie imaginaire. Attention, la partie imaginaire est b et non bi.