Exercices Corrigés : Probabilité d'un Événement

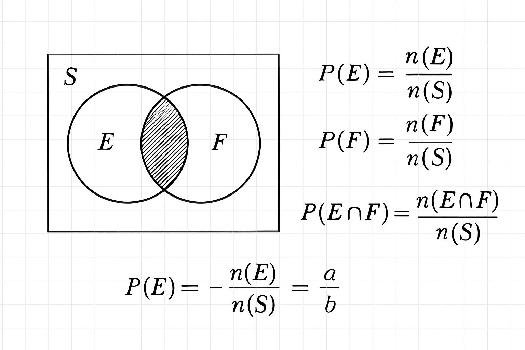
Exercice 1 : Lancer de deux dés

On lance deux dés à six faces non truqués. Quelle est la probabilité d'obtenir une somme égale à 7 ?

Solution :
L'univers des possibles (Ω) est l'ensemble de toutes les paires possibles de résultats des deux dés. Il y a 6 * 6 = 36 résultats possibles.
L'événement A = 'Obtenir une somme égale à 7' est représenté par les paires suivantes : (1, 6), (2, 5), (3, 4), (4, 3), (5, 2), (6, 1). Il y a 6 cas favorables.
P(A) = 6/36 = 1/6.

Exercice 2 : Tirage de boules dans une urne

Une urne contient 5 boules rouges et 3 boules bleues. On tire une boule au hasard. Quelle est la probabilité de tirer une boule bleue ?

Solution :
Le nombre total de boules est 5 + 3 = 8.
L'événement A = 'Tirer une boule bleue'. Il y a 3 boules bleues.
P(A) = 3/8.

Exercice 3 : Probabilité conditionnelle

Dans une classe, 60% des élèves aiment les maths et 70% aiment la physique. 40% aiment les deux matières. Quelle est la probabilité qu'un élève aime les maths sachant qu'il aime la physique ?

Solution :
Soit M l'événement 'l'élève aime les maths' et P l'événement 'l'élève aime la physique'.
On cherche P(M|P), la probabilité de M sachant P.
P(M|P) = P(M ∩ P) / P(P)
P(M ∩ P) = 0.4
P(P) = 0.7
P(M|P) = 0.4 / 0.7 = 4/7.

Exercice 4 : Événements indépendants

On lance une pièce de monnaie deux fois. Quelle est la probabilité d'obtenir Pile au premier lancer et Face au deuxième lancer ?

Solution :
Les deux lancers sont indépendants. La probabilité d'obtenir Pile au premier lancer est 1/2. La probabilité d'obtenir Face au deuxième lancer est 1/2.
P(Pile au 1er lancer et Face au 2ème lancer) = (1/2) * (1/2) = 1/4.

Exercice 5 : Evenements incompatibles

Une urne contient 4 boules vertes et 6 boules jaunes. On tire une boule au hasard. Soit A l'événement 'tirer une boule verte' et B l'événement 'tirer une boule jaune'. Calculer P(A∪B)

Solution :
Les événements A et B sont incompatibles (on ne peut pas tirer une boule qui soit à la fois verte et jaune).
P(A) = 4/10
P(B) = 6/10
P(A∪B) = P(A) + P(B) = 4/10 + 6/10 = 1.

Ce qu'il faut retenir

• Pour résoudre un problème de probabilité, il faut d'abord bien définir l'univers des possibles et l'événement concerné.
• Identifier si les événements sont indépendants, incompatibles, ou compatibles.
• Utiliser les formules appropriées pour calculer les probabilités.
• Penser à simplifier les fractions pour obtenir une réponse plus claire.