Équations de Droites : Cartésiennes et Paramétriques

Introduction aux Droites dans le Plan

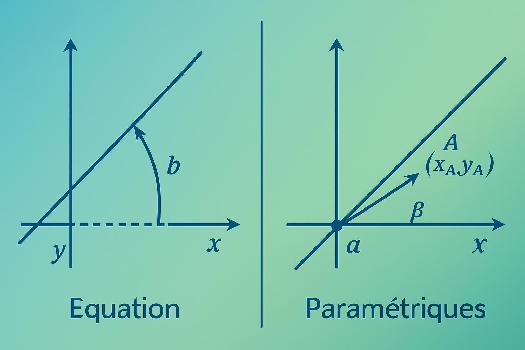
Dans le plan, une droite est un ensemble infini de points alignés. Pour décrire une droite de manière précise, on utilise des équations. Il existe principalement deux types d'équations pour représenter une droite : les équations cartésiennes et les équations paramétriques. Comprendre ces deux formes est essentiel pour résoudre des problèmes de géométrie.

Équation Cartésienne d'une Droite

Forme générale : L'équation cartésienne d'une droite dans le plan est de la forme ax + by + c = 0, où a, b et c sont des nombres réels et (a, b) ≠ (0, 0). Les coefficients a et b sont liés au vecteur normal de la droite.

Vecteur Normal : Un vecteur normal à la droite est un vecteur perpendiculaire à la droite. Ses coordonnées sont (a, b).

Exemple : Considérons la droite d'équation 2x + 3y - 6 = 0. Ici, a = 2, b = 3 et c = -6. Le vecteur normal à cette droite est (2, 3).

Détermination de l'équation cartésienne à partir de deux points : Si on connaît deux points A(x_A, y_A) et B(x_B, y_B) appartenant à la droite, on peut trouver l'équation cartésienne. Le vecteur directeur de la droite est AB(x_B - x_A, y_B - y_A), et le vecteur normal est (- (y_B - y_A), x_B - x_A).

Exemple : Soient A(1, 2) et B(4, 5). AB(3, 3), vecteur normal (-3, 3). L'équation est de la forme -3x + 3y + c = 0. En remplaçant par A(1, 2), on obtient -3(1) + 3(2) + c = 0, donc c = -3. L'équation est -3x + 3y - 3 = 0, qu'on peut simplifier en -x + y - 1 = 0.

Équations Paramétriques d'une Droite

Principe : Les équations paramétriques expriment les coordonnées x et y des points de la droite en fonction d'un paramètre t (nombre réel).

Forme générale : Une droite passant par un point A(x_A, y_A) et de vecteur directeur u(α, β) a pour équations paramétriques :
x = x_A + tα
y = y_A + tβ
où t ∈ ℝ.

Vecteur Directeur : Le vecteur directeur u(α, β) donne la direction de la droite.

Exemple : Soit la droite passant par A(2, 1) et de vecteur directeur u(1, -1). Les équations paramétriques sont :
x = 2 + t
y = 1 - t
où t ∈ ℝ.

Passage des équations paramétriques à l'équation cartésienne : On peut éliminer le paramètre t pour obtenir l'équation cartésienne. Dans l'exemple précédent, on a t = x - 2 et t = 1 - y. Donc, x - 2 = 1 - y, ce qui donne x + y - 3 = 0.

Interprétation Géométrique

Équation Cartésienne : L'équation cartésienne met en évidence la relation linéaire entre x et y qui définit tous les points de la droite. Elle est pratique pour déterminer si un point appartient à la droite ou pour trouver l'intersection de deux droites.

Équations Paramétriques : Les équations paramétriques offrent une manière de 'parcourir' la droite en faisant varier le paramètre t. Chaque valeur de t correspond à un point spécifique sur la droite. Elles sont utiles pour décrire le mouvement d'un point le long de la droite.

Exemples et Applications

Exemple 1 : Trouver l'équation cartésienne de la droite passant par A(3, 4) et de vecteur directeur u(2, 1). On cherche d'abord un vecteur normal, par exemple (-1, 2). L'équation est de la forme -x + 2y + c = 0. En remplaçant par A(3, 4), -3 + 8 + c = 0, donc c = -5. L'équation est -x + 2y - 5 = 0.

Exemple 2 : Trouver les équations paramétriques de la droite d'équation cartésienne x - 2y + 1 = 0. On peut exprimer x en fonction de y : x = 2y - 1. En posant y = t, on a x = 2t - 1. Les équations paramétriques sont :
x = 2t - 1
y = t
où t ∈ ℝ.

Application : Déterminer si le point C(5, 3) appartient à la droite d'équation 2x - y - 7 = 0. On remplace x et y par les coordonnées de C : 2(5) - 3 - 7 = 10 - 3 - 7 = 0. Donc, C appartient à la droite.

Positions Relatives de Deux Droites

Deux droites dans le plan peuvent être :

Sécantes : Elles se coupent en un seul point. Pour trouver le point d'intersection, on résout le système d'équations formé par leurs équations cartésiennes ou paramétriques.

Parallèles : Elles ont la même direction (vecteurs directeurs colinéaires) et ne se coupent pas. Leurs vecteurs normaux sont également colinéaires.

Confondus : Elles représentent la même droite (équations cartésiennes proportionnelles ou mêmes équations paramétriques à un changement de paramètre près).

Orthogonales (perpendiculaires) : Leurs vecteurs directeurs (ou normaux) sont orthogonaux, c'est-à-dire que leur produit scalaire est nul.

Ce qu'il faut retenir

• Équation cartésienne : ax + by + c = 0 (où (a, b) est un vecteur normal).
• Équations paramétriques : x = x_A + tα, y = y_A + tβ (où A(x_A, y_A) est un point de la droite et (α, β) un vecteur directeur).
• Pour trouver l'équation cartésienne à partir de deux points, on calcule le vecteur directeur puis un vecteur normal.
• Pour passer des équations paramétriques à l'équation cartésienne, on élimine le paramètre t.
• Deux droites sont parallèles si leurs vecteurs directeurs sont colinéaires.
• Deux droites sont perpendiculaires si le produit scalaire de leurs vecteurs directeurs est nul.