Le Produit Scalaire : Guide Complet pour le Lycée

Définition du Produit Scalaire

Le produit scalaire de deux vecteurs $\vec{u}$ et $\vec{v}$, noté $\vec{u} \cdot \vec{v}$, est un nombre réel. Il peut être défini de deux manières principales :

1. Définition géométrique : $\vec{u} \cdot \vec{v} = ||\vec{u}|| \cdot ||\vec{v}|| \cdot cos(\theta)$, où $||\vec{u}||$ et $||\vec{v}||$ sont les normes (longueurs) des vecteurs $\vec{u}$ et $\vec{v}$ respectivement, et $\theta$ est l'angle entre les deux vecteurs.
2. Définition analytique (dans un repère orthonormé) : Si $\vec{u}(x_u, y_u)$ et $\vec{v}(x_v, y_v)$, alors $\vec{u} \cdot \vec{v} = x_u x_v + y_u y_v$.

Propriétés Fondamentales du Produit Scalaire

Le produit scalaire possède plusieurs propriétés essentielles qui facilitent son utilisation :

• Commutativité : $\vec{u} \cdot \vec{v} = \vec{v} \cdot \vec{u}$. L'ordre des vecteurs n'affecte pas le résultat.
• Distributivité par rapport à l'addition vectorielle : $\vec{u} \cdot (\vec{v} + \vec{w}) = \vec{u} \cdot \vec{v} + \vec{u} \cdot \vec{w}$.
• Associativité par rapport à la multiplication par un scalaire : $(\lambda \vec{u}) \cdot \vec{v} = \lambda (\vec{u} \cdot \vec{v})$, où $\lambda$ est un nombre réel.
• Produit scalaire d'un vecteur avec lui-même : $\vec{u} \cdot \vec{u} = ||\vec{u}||^2$. Cela est égal au carré de la norme du vecteur.

Applications du Produit Scalaire

Le produit scalaire trouve des applications dans divers domaines de la géométrie et au-delà :

1. Calcul d'angles : Connaissant les vecteurs $\vec{u}$ et $\vec{v}$, on peut déterminer l'angle $\theta$ entre eux en utilisant la formule $\cos(\theta) = \frac{\vec{u} \cdot \vec{v}}{||\vec{u}|| \cdot ||\vec{v}||}$. Cela est particulièrement utile pour déterminer si deux vecteurs sont orthogonaux. Si $\vec{u} \cdot \vec{v} = 0$, alors $\vec{u}$ et $\vec{v}$ sont orthogonaux (l'angle entre eux est de 90 degrés).
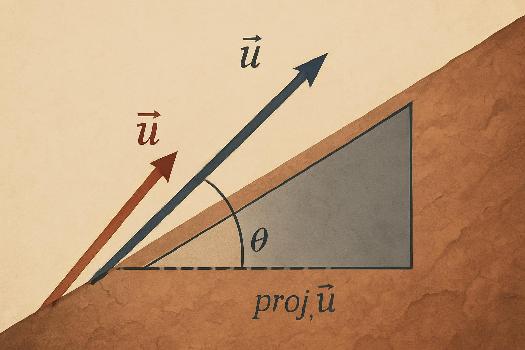
2. Projection orthogonale : Le produit scalaire permet de calculer la projection d'un vecteur $\vec{u}$ sur un vecteur $\vec{v}$. La projection orthogonale de $\vec{u}$ sur $\vec{v}$ est donnée par $\text{proj}_\vec{v} \vec{u} = \frac{\vec{u} \cdot \vec{v}}{||\vec{v}||^2} \vec{v}$.
3. Détermination de l'orthogonalité : Comme mentionné précédemment, si $\vec{u} \cdot \vec{v} = 0$, alors $\vec{u}$ et $\vec{v}$ sont orthogonaux. Cela est fondamental pour vérifier la perpendicularité de droites ou de plans.
4. Travail d'une force (en physique) : En physique, le travail $W$ effectué par une force $\vec{F}$ lors d'un déplacement $\vec{d}$ est donné par $W = \vec{F} \cdot \vec{d}$.

Exemples Concrets

Exemple 1 : Calcul de l'angle entre deux vecteurs Soient $\vec{u}(2, 3)$ et $\vec{v}(-1, 4)$. Calculons l'angle entre eux. $\vec{u} \cdot \vec{v} = (2)(-1) + (3)(4) = -2 + 12 = 10$. $||\vec{u}|| = \sqrt{2^2 + 3^2} = \sqrt{13}$. $||\vec{v}|| = \sqrt{(-1)^2 + 4^2} = \sqrt{17}$. $\cos(\theta) = \frac{10}{\sqrt{13} \cdot \sqrt{17}} \approx \frac{10}{14.87} \approx 0.672$. $\theta = \arccos(0.672) \approx 47.8°$. Exemple 2 : Vérification de l'orthogonalité Soient $\vec{a}(1, -2)$ et $\vec{b}(4, 2)$. Vérifions si ces vecteurs sont orthogonaux. $\vec{a} \cdot \vec{b} = (1)(4) + (-2)(2) = 4 - 4 = 0$. Puisque le produit scalaire est nul, les vecteurs $\vec{a}$ et $\vec{b}$ sont orthogonaux.

Ce qu'il faut retenir

• Définition : $\vec{u} \cdot \vec{v} = ||\vec{u}|| \cdot ||\vec{v}|| \cdot cos(\theta)$ (géométrique) ou $\vec{u} \cdot \vec{v} = x_u x_v + y_u y_v$ (analytique).
• Commutativité : $\vec{u} \cdot \vec{v} = \vec{v} \cdot \vec{u}$.
• Distributivité : $\vec{u} \cdot (\vec{v} + \vec{w}) = \vec{u} \cdot \vec{v} + \vec{u} \cdot \vec{w}$.
• Orthogonalité : Si $\vec{u} \cdot \vec{v} = 0$, alors $\vec{u}$ et $\vec{v}$ sont orthogonaux.
• Calcul d'angle : $\cos(\theta) = \frac{\vec{u} \cdot \vec{v}}{||\vec{u}|| \cdot ||\vec{v}||}$.
• Projection : $\text{proj}_\vec{v} \vec{u} = \frac{\vec{u} \cdot \vec{v}}{||\vec{v}||^2} \vec{v}$.