Mathématiques > Géométrie > Géométrie Spatiale > Distance d'un point à une droite, d'un point à un plan

Distance d'un Point à une Droite et d'un Point à un Plan

Apprenez à calculer la distance d'un point à une droite et d'un point à un plan en géométrie spatiale. Ce guide complet, avec des exemples détaillés, est conçu pour les élèves de lycée.

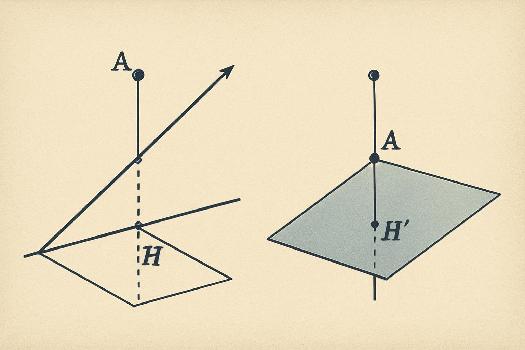
Distance d'un Point à une Droite

La distance d'un point A à une droite (d) est la plus courte distance entre ce point et un point quelconque de la droite. Il s'agit de la longueur du segment AH où H est le projeté orthogonal de A sur la droite (d). Méthode de calcul :

  1. Déterminer une représentation paramétrique de la droite (d). Par exemple, (d) : M(t) = B + t*u où B est un point de la droite et u est un vecteur directeur.
  2. Exprimer le vecteur AM(t). Où A est le point dont on veut calculer la distance à la droite.
  3. Imposer que le vecteur AM(t) soit orthogonal au vecteur directeur u. Cela se traduit par l'équation AM(t) . u = 0 (produit scalaire nul).
  4. Résoudre l'équation pour trouver la valeur de t. On obtient ainsi la valeur de t0 correspondant au point H, projeté orthogonal de A sur (d).
  5. Calculer les coordonnées de H. En remplaçant t0 dans la représentation paramétrique de la droite.
  6. Calculer la distance AH. AH = ||AM(t0)||, c'est-à-dire la norme du vecteur AH.
Exemple : Soit le point A(1, 2, 3) et la droite (d) passant par B(0, 1, 1) et de vecteur directeur u(1, 0, 1).
  1. Représentation paramétrique de (d) : M(t) = (0, 1, 1) + t(1, 0, 1) = (t, 1, 1+t)
  2. AM(t) = (t-1, -1, t-2)
  3. AM(t) . u = (t-1)*1 + (-1)*0 + (t-2)*1 = 2t - 3 = 0
  4. t = 3/2
  5. H = (3/2, 1, 5/2)
  6. AH = ||(1/2, -1, -1/2)|| = √(1/4 + 1 + 1/4) = √(6/4) = √6 / 2

Distance d'un Point à un Plan

La distance d'un point A à un plan (P) est la plus courte distance entre ce point et un point quelconque du plan. C'est la longueur du segment AH où H est le projeté orthogonal de A sur le plan (P). Méthode de calcul :

  1. Déterminer une équation cartésienne du plan (P). Sous la forme ax + by + cz + d = 0.
  2. Connaître les coordonnées du point A. Soit A(xA, yA, zA).
  3. Appliquer la formule : d(A, (P)) = |axA + byA + czA + d| / √(a2 + b2 + c2) où :
    • d(A, (P)) est la distance du point A au plan (P).
    • |...| indique la valeur absolue.
    • a, b, c sont les coefficients de l'équation cartésienne du plan.
    • xA, yA, zA sont les coordonnées du point A.
Exemple : Soit le point A(1, 2, 3) et le plan (P) d'équation 2x - y + 2z + 1 = 0. d(A, (P)) = |2*1 - 1*2 + 2*3 + 1| / √(22 + (-1)2 + 22) = |2 - 2 + 6 + 1| / √(4 + 1 + 4) = 7 / √9 = 7 / 3

Projeté orthogonal

Le projeté orthogonal d'un point A sur une droite (ou un plan) est le point H de cette droite (ou de ce plan) tel que la droite (AH) soit perpendiculaire à la droite (ou au plan) considéré. C'est un concept fondamental pour comprendre et calculer les distances.

Vecteur directeur et vecteur normal

Un vecteur directeur d'une droite est un vecteur non nul qui indique la direction de cette droite. Un vecteur normal d'un plan est un vecteur non nul qui est perpendiculaire à ce plan. Il est essentiel pour définir l'équation cartésienne d'un plan.

Ce qu'il faut retenir

  • Distance Point-Droite : C'est la longueur du segment [AH], où H est le projeté orthogonal de A sur la droite. On utilise une représentation paramétrique de la droite, on exprime le vecteur AM(t), on impose l'orthogonalité avec le vecteur directeur, et on calcule la distance AH.
  • Distance Point-Plan : On utilise la formule d(A, (P)) = |axA + byA + czA + d| / √(a2 + b2 + c2), où ax + by + cz + d = 0 est l'équation cartésienne du plan.
  • Projeté orthogonal : Le point sur la droite ou le plan le plus proche du point donné, formant un angle droit.
  • Vecteur directeur et normal : Essentiels pour définir les directions et orientations des droites et des plans.

← Comprendre le Cosinus, le Sinus et la Tangente d'un Angle Distance entre deux points dans un repère orthonormé →

FAQ

  • Comment trouver le projeté orthogonal d'un point sur une droite ?

    Il faut utiliser la représentation paramétrique de la droite. Le projeté est le point de la droite qui minimise la distance au point donné. Cela revient à résoudre une équation obtenue en imposant l'orthogonalité entre le vecteur reliant le point à un point générique de la droite et le vecteur directeur de la droite.
  • Que faire si l'équation cartésienne du plan n'est pas donnée ?

    Si vous avez trois points non alignés du plan, vous pouvez déterminer deux vecteurs directeurs du plan. Ensuite, vous pouvez calculer le produit vectoriel de ces deux vecteurs pour obtenir un vecteur normal au plan. Enfin, en utilisant un point du plan et le vecteur normal, vous pouvez déterminer l'équation cartésienne du plan.
  • La distance d'un point à une droite ou un plan peut-elle être négative ?

    Non, la distance est toujours une valeur positive ou nulle. C'est pourquoi on utilise la valeur absolue dans la formule de la distance d'un point à un plan.