Mathématiques > Calcul Matriciel (Terminale - Spécialité) > Déterminants et Inverses > Résolution de systèmes linéaires à l'aide des matrices
Résolution de systèmes linéaires à l'aide des matrices
Apprenez à résoudre des systèmes d'équations linéaires en utilisant les matrices, une méthode puissante et élégante. Ce guide vous explique étape par étape comment représenter un système sous forme matricielle, calculer l'inverse d'une matrice (si possible) et trouver la solution du système. Des exemples concrets illustrent chaque étape pour une compréhension facile et approfondie.
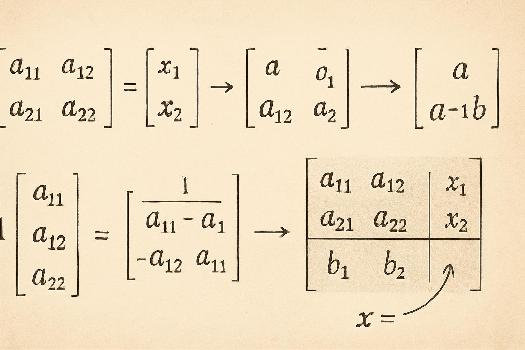
Introduction aux systèmes d'équations linéaires et aux matrices
La résolution de systèmes d'équations linéaires est un problème fondamental en mathématiques. Un système d'équations linéaires est un ensemble d'équations dans lesquelles les inconnues apparaissent au premier degré. Par exemple: <ul> <li>2x + y = 5</li> <li>x - y = 1</li> </ul> Les matrices offrent un moyen élégant et efficace de résoudre ces systèmes. Une matrice est un tableau rectangulaire de nombres. Nous pouvons représenter un système d'équations linéaires sous forme matricielle. Cela nous permet d'appliquer des opérations matricielles pour résoudre le système.
Représentation matricielle d'un système d'équations linéaires
Un système d'équations linéaires peut être représenté sous la forme matricielle Ax = b, où: <ul> <li>A est la matrice des coefficients du système.</li> <li>x est la matrice des inconnues.</li> <li>b est la matrice des termes constants.</li> </ul> Reprenons l'exemple précédent: <ul> <li>2x + y = 5</li> <li>x - y = 1</li> </ul> La représentation matricielle est: <table> <tr> <td>A = </td> <td> <img src='https://i.imgur.com/0U1Tq7b.png' width='50px'> </td> </tr> <tr> <td>x = </td> <td> <img src='https://i.imgur.com/N7c4x18.png' width='30px'> </td> </tr> <tr> <td>b = </td> <td> <img src='https://i.imgur.com/fW6x8pD.png' width='30px'> </td> </tr> </table> Donc, Ax = b s'écrit: <img src='https://i.imgur.com/r9zYwD6.png' width='150px'>
Résolution à l'aide de l'inverse de la matrice
Si la matrice A est inversible (c'est-à-dire, si son déterminant est non nul), alors le système Ax = b admet une solution unique donnée par: x = A-1b Où A-1 est la matrice inverse de A. <strong>Étape 1: Calcul de l'inverse de A</strong> Pour une matrice 2x2 comme dans notre exemple, l'inverse se calcule facilement: Si A = <img src='https://i.imgur.com/0U1Tq7b.png' width='50px'> alors A-1 = (1/det(A)) * <img src='https://i.imgur.com/9c4yV70.png' width='50px'> Où det(A) est le déterminant de A. Dans notre exemple, det(A) = (2 * -1) - (1 * 1) = -3. Ainsi, A-1 = (-1/3) * <img src='https://i.imgur.com/9c4yV70.png' width='50px'> = <img src='https://i.imgur.com/aXk0J4i.png' width='90px'> <strong>Étape 2: Calcul de la solution x</strong> Maintenant, calculons x = A-1b: x = <img src='https://i.imgur.com/aXk0J4i.png' width='90px'> * <img src='https://i.imgur.com/fW6x8pD.png' width='30px'> = <img src='https://i.imgur.com/tqJ5g21.png' width='45px'> Donc, x = 2 et y = 1. La solution du système est (2, 1).
Cas où la matrice n'est pas inversible
Si le déterminant de la matrice A est nul (det(A) = 0), alors la matrice A n'est pas inversible. Dans ce cas, le système d'équations linéaires peut avoir soit aucune solution (système incompatible), soit une infinité de solutions (système indéterminé). Pour déterminer le nombre de solutions et les trouver, on peut utiliser la méthode du pivot de Gauss (élimination de Gauss-Jordan). Cette méthode consiste à transformer la matrice augmentée [A|b] en une matrice échelonnée réduite en utilisant des opérations élémentaires sur les lignes.
Ce qu'il faut retenir
<ul> <li>Un système d'équations linéaires peut être représenté sous la forme matricielle Ax = b.</li> <li>Si la matrice A est inversible, la solution du système est x = A-1b.</li> <li>Pour trouver l'inverse d'une matrice 2x2, on utilise la formule: Si A = <img src='https://i.imgur.com/0U1Tq7b.png' width='50px'> alors A-1 = (1/det(A)) * <img src='https://i.imgur.com/9c4yV70.png' width='50px'></li> <li>Si la matrice A n'est pas inversible (det(A) = 0), le système peut avoir soit aucune solution, soit une infinité de solutions. Dans ce cas, on utilise la méthode du pivot de Gauss.</li> </ul>
FAQ
-
Comment savoir si une matrice est inversible?
Une matrice est inversible si et seulement si son déterminant est non nul. -
Que faire si la matrice n'est pas inversible?
Si la matrice n'est pas inversible, vous pouvez utiliser la méthode du pivot de Gauss pour déterminer si le système a des solutions et, le cas échéant, les trouver. -
La méthode de l'inverse matriciel fonctionne-t-elle pour tous les systèmes d'équations linéaires?
Non, elle ne fonctionne que si la matrice des coefficients est carrée et inversible (son déterminant est non nul).
