Mathématiques > Analyse > Intégration > Théorème fondamental de l'analyse
Théorème Fondamental de l'Analyse : Un Guide Complet
Comprendre le Théorème Fondamental de l'Analyse (TFA) : lien entre dérivation et intégration. Explications détaillées, exemples concrets et exercices pour les élèves de lycée.
Introduction : Le Lien Entre Dérivation et Intégration
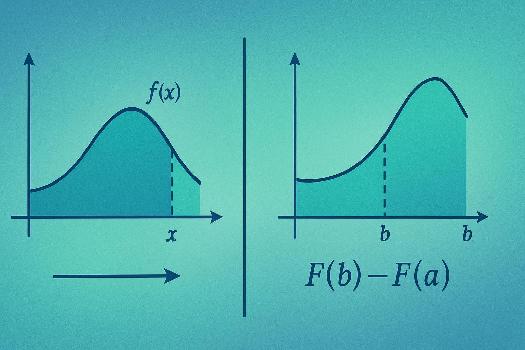
Bienvenue dans le monde fascinant du Théorème Fondamental de l'Analyse ! Ce théorème est un pilier de l'analyse mathématique car il établit un lien profond et fondamental entre deux opérations qui peuvent sembler distinctes au premier abord : la dérivation et l'intégration. Imaginez la dérivation comme l'opération qui calcule la pente d'une courbe en un point donné, et l'intégration comme l'opération qui calcule l'aire sous cette même courbe. Le TFA nous dit que ces deux opérations sont, en quelque sorte, inverses l'une de l'autre. Autrement dit, l'intégrale d'une fonction peut être calculée en trouvant une fonction dont la dérivée est la fonction d'origine.
Première Partie du Théorème : L'Intégrale Indéfinie et sa Dérivée
La première partie du TFA stipule que si une fonction f est continue sur un intervalle [a, b], alors la fonction F définie par F(x) = ∫ax f(t) dt est dérivable sur [a, b], et sa dérivée est égale à f(x). En termes plus simples, si vous intégrez une fonction continue f de a à x, et que vous dérivez ensuite le résultat par rapport à x, vous obtenez simplement la fonction originale f(x).
Exemple : Soit f(t) = t2. Alors F(x) = ∫0x t2 dt = [t3/3]0x = x3/3. Maintenant, dérivons F(x): F'(x) = d/dx (x3/3) = x2 = f(x). Comme vous pouvez le voir, la dérivée de l'intégrale est égale à la fonction originale.
Deuxième Partie du Théorème : Le Calcul des Intégrales Définies
La deuxième partie du TFA nous donne un moyen puissant de calculer les intégrales définies. Elle stipule que si f est continue sur [a, b] et F est une primitive de f (c'est-à-dire, F'(x) = f(x)), alors ∫ab f(x) dx = F(b) - F(a). En d'autres termes, pour calculer l'intégrale définie de f de a à b, il suffit de trouver une primitive F de f, d'évaluer F en b et en a, et de soustraire les deux résultats.
Exemple : Calculons l'intégrale de x2 de 1 à 3. Nous savons que F(x) = x3/3 est une primitive de x2. Donc, ∫13 x2 dx = F(3) - F(1) = (33/3) - (13/3) = 9 - 1/3 = 26/3.
Preuve Simplifiée du Théorème
Bien qu'une preuve rigoureuse nécessite des concepts d'analyse avancés, on peut comprendre l'intuition derrière le TFA de la manière suivante :
Considérez l'intégrale ∫ax f(t) dt comme l'aire sous la courbe de f entre a et x. Si l'on augmente x d'une petite quantité Δx, l'aire supplémentaire ajoutée est approximativement f(x)Δx (l'aire d'un rectangle de hauteur f(x) et de largeur Δx). Donc, le changement de l'aire (c'est-à-dire, F(x + Δx) - F(x)) est approximativement f(x)Δx. En divisant par Δx et en prenant la limite lorsque Δx tend vers zéro, on obtient F'(x) = f(x), ce qui est la première partie du TFA.
Applications du Théorème Fondamental de l'Analyse
Le TFA est un outil essentiel dans de nombreux domaines des mathématiques, de la physique et de l'ingénierie. Voici quelques exemples :
- Calcul d'aires et de volumes : Le TFA permet de calculer précisément les aires de régions complexes et les volumes de solides.
- Résolution d'équations différentielles : De nombreuses équations différentielles peuvent être résolues en utilisant le TFA pour trouver des primitives.
- Modélisation de phénomènes physiques : Le TFA est utilisé pour modéliser des phénomènes tels que le mouvement d'un objet sous l'influence d'une force, ou la variation de la température dans un matériau.
Exemples d'Exercices Corrigés
Voici quelques exercices pour vous aider à maîtriser le TFA :
Exercice 1 : Calculer la dérivée de F(x) = ∫0x sin(t) dt.
Solution : D'après la première partie du TFA, F'(x) = sin(x).
Exercice 2 : Calculer l'intégrale de 2x de 0 à 2.
Solution : Une primitive de 2x est x2. Donc, ∫02 2x dx = 22 - 02 = 4.
Ce qu'il faut retenir
- Le Théorème Fondamental de l'Analyse (TFA) relie la dérivation et l'intégration.
- Première partie du TFA : Si f est continue, alors la dérivée de ∫ax f(t) dt est f(x).
- Deuxième partie du TFA : Si F est une primitive de f, alors ∫ab f(x) dx = F(b) - F(a).
- Le TFA est utilisé pour calculer des intégrales définies et résoudre des équations différentielles.
FAQ
-
Quelle est la différence entre une intégrale définie et une intégrale indéfinie ?
Une intégrale indéfinie est une fonction dont la dérivée est la fonction donnée. Elle est représentée par ∫ f(x) dx et a une infinité de solutions (différentes par une constante). Une intégrale définie est un nombre qui représente l'aire sous la courbe de la fonction entre deux bornes données. Elle est représentée par ∫ab f(x) dx. -
Comment trouver une primitive d'une fonction ?
Trouver une primitive d'une fonction peut être difficile, mais il existe quelques techniques courantes :- Utiliser des tableaux de primitives : De nombreux tableaux répertorient les primitives des fonctions courantes.
- Utiliser la règle de puissance inverse : Si f(x) = xn, alors une primitive est F(x) = xn+1/(n+1) (sauf si n = -1).
- Utiliser l'intégration par parties : Cette technique est utile pour intégrer des produits de fonctions.
- Utiliser la substitution : Cette technique consiste à changer la variable d'intégration pour simplifier l'intégrale.
