Mathématiques > Algèbre > Équations et Inéquations > Inéquations du second degré

Résoudre les Inéquations du Second Degré : Guide Pas à Pas

Apprenez à résoudre les inéquations du second degré avec cette méthode détaillée. Comprenez le rôle du discriminant, trouvez les racines et déterminez les intervalles de solutions. Parfait pour les lycéens préparant le bac !

Introduction aux Inéquations du Second Degré

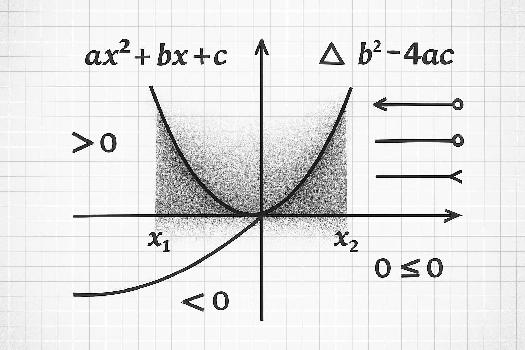
Une inéquation du second degré est une inégalité qui peut être mise sous la forme ax2 + bx + c > 0, ax2 + bx + c < 0, ax2 + bx + c ≥ 0, ou ax2 + bx + c ≤ 0, où a, b, et c sont des constantes et a ≠ 0. Résoudre une inéquation du second degré consiste à trouver tous les x qui vérifient l'inégalité.

La méthode de résolution repose sur l'étude du signe du trinôme ax2 + bx + c. On commence par trouver les racines de l'équation ax2 + bx + c = 0, puis on étudie le signe du trinôme entre et en dehors de ces racines.

Étape 1: Calcul du Discriminant (Δ)

Le discriminant, noté Δ (delta), est donné par la formule: Δ = b2 - 4ac. Il permet de déterminer le nombre de racines réelles de l'équation ax2 + bx + c = 0 et donc la forme du trinôme. Il existe trois cas possibles:

  • Δ > 0: L'équation a deux racines réelles distinctes.
  • Δ = 0: L'équation a une racine réelle double.
  • Δ < 0: L'équation n'a pas de racine réelle.

Étape 2: Trouver les Racines (si Δ ≥ 0)

Si Δ ≥ 0, on calcule les racines de l'équation ax2 + bx + c = 0. Si Δ > 0, les racines sont données par:

x1 = (-b - √Δ) / 2a et x2 = (-b + √Δ) / 2a

Si Δ = 0, il y a une seule racine (double) donnée par:

x = -b / 2a

Ces racines sont cruciales car elles délimitent les intervalles où le trinôme change de signe.

Étape 3: Étude du Signe du Trinôme

Une fois les racines trouvées (si elles existent), on étudie le signe du trinôme ax2 + bx + c sur les différents intervalles définis par ces racines. Le signe du trinôme est déterminé par le signe de a:

  • Si a > 0: Le trinôme est positif à l'extérieur des racines (si elles existent) et négatif entre les racines.
  • Si a < 0: Le trinôme est négatif à l'extérieur des racines (si elles existent) et positif entre les racines.

Il est souvent utile de construire un tableau de signes pour visualiser le signe du trinôme sur les différents intervalles.

Étape 4: Conclusion et Intervalles de Solutions

En se basant sur le tableau de signes, on détermine les intervalles de x qui satisfont l'inéquation de départ (ax2 + bx + c > 0, ax2 + bx + c < 0, ax2 + bx + c ≥ 0, ou ax2 + bx + c ≤ 0). Il faut faire attention à inclure ou exclure les racines selon que l'inégalité est stricte (> ou <) ou large (≥ ou ≤).

Exemple Concret

Résolvons l'inéquation: x2 - 3x + 2 > 0

1. Calcul du discriminant: Δ = (-3)2 - 4 * 1 * 2 = 9 - 8 = 1 > 0
2. Racines: x1 = (3 - √1) / 2 = 1 et x2 = (3 + √1) / 2 = 2
3. Signe du trinôme: Comme a = 1 > 0, le trinôme est positif à l'extérieur des racines (x < 1 ou x > 2) et négatif entre les racines (1 < x < 2).
4. Conclusion: La solution de l'inéquation est x ∈ ]-∞, 1[ ∪ ]2, +∞[.

Ce qu'il faut retenir

  • Une inéquation du second degré a la forme ax2 + bx + c > 0 (ou <, ≥, ≤).
  • Le discriminant Δ = b2 - 4ac détermine le nombre de racines: Δ > 0 (2 racines), Δ = 0 (1 racine double), Δ < 0 (pas de racines réelles).
  • Les racines délimitent les intervalles où le trinôme change de signe.
  • Le signe de 'a' détermine le signe du trinôme à l'extérieur et entre les racines.
  • Il faut bien identifier les intervalles qui correspondent à la solution de l'inéquation.

← Résolution graphique d'équations et d'inéquations : Une approche visuelle Résoudre une Équation du Premier Degré : Guide Complet →

FAQ

  • Que faire si le discriminant est négatif ?

    Si le discriminant est négatif (Δ < 0), cela signifie que l'équation ax2 + bx + c = 0 n'a pas de racines réelles. Dans ce cas, le signe du trinôme ax2 + bx + c est constant et est le même que le signe de a. Il suffit alors de vérifier si ce signe constant satisfait l'inéquation.
  • Comment gérer les inégalités larges (≥ ou ≤) ?

    Pour les inégalités larges, il faut inclure les racines dans les intervalles de solutions. Par exemple, si on a ax2 + bx + c ≥ 0, les racines pour lesquelles ax2 + bx + c = 0 sont également des solutions.