Mathématiques > Analyse > Dérivation > Nombre dérivé et tangente

Exercices corrigés : Nombre dérivé et tangente

Entraînez-vous avec des exercices corrigés sur le nombre dérivé, le calcul de tangentes et leurs applications. Idéal pour la préparation aux examens.

Exercice 1 : Calcul du nombre dérivé et de l'équation de la tangente

Énoncé: Soit f(x) = x3 - 2x. Calculer f'(1) et donner l'équation de la tangente à la courbe de f au point d'abscisse 1.

Solution:
1. Calculons f'(x): f'(x) = 3x2 - 2
2. Calculons f'(1): f'(1) = 3(1)2 - 2 = 1
3. Calculons f(1): f(1) = (1)3 - 2(1) = -1
4. L'équation de la tangente est: y = f'(1)(x - 1) + f(1) = 1(x - 1) - 1 = x - 2

Exercice 2 : Interprétation graphique du nombre dérivé

Énoncé: La courbe ci-dessous représente une fonction g. Estimer graphiquement g'(2) et expliquer sa signification.

[Image d'une courbe avec une tangente tracée au point d'abscisse 2, avec une pente approximative de 0.5]

Solution: g'(2) est la pente de la tangente à la courbe de g au point d'abscisse 2. D'après le graphique, la pente de la tangente est approximativement 0.5. Cela signifie que au point x=2, la fonction g est croissante et que pour une petite variation de x autour de 2, la fonction g augmente d'environ la moitié de cette variation.

Exercice 3 : Utilisation du nombre dérivé pour trouver un extremum

Énoncé: Soit h(x) = -x2 + 4x + 1. Trouver les extremums de h(x).

Solution:
1. Calculons h'(x): h'(x) = -2x + 4
2. Trouvons les points où h'(x) = 0: -2x + 4 = 0 => x = 2
3. Déterminons la nature de l'extremum. Calculons h''(x): h''(x) = -2. Comme h''(2) = -2 < 0, x = 2 est un maximum.
4. Calculons la valeur du maximum: h(2) = -(2)2 + 4(2) + 1 = 5

Donc, h(x) admet un maximum en x = 2, et la valeur de ce maximum est 5.

Ce qu'il faut retenir

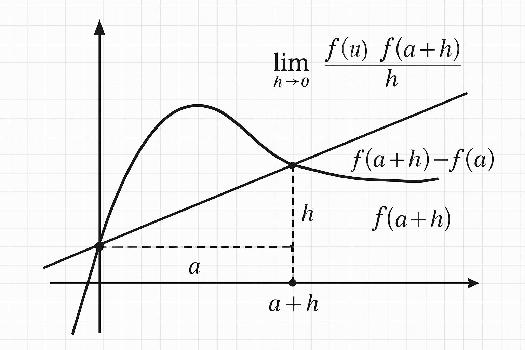
  • Le nombre dérivé se calcule à l'aide de la formule lim (h -> 0) [f(a + h) - f(a)] / h
  • La tangente à la courbe en un point a pour équation y = f'(a)(x - a) + f(a)
  • Les extremums d'une fonction se trouvent en résolvant f'(x) = 0

← Exercices Corrigés sur les Dérivées des Fonctions Usuelles Exercices corrigés : Sens de variation d'une fonction et signe de sa dérivée →

FAQ

  • Comment savoir si un point critique est un maximum ou un minimum ?

    On peut utiliser le signe de la dérivée seconde. Si f''(x) > 0, c'est un minimum. Si f''(x) < 0, c'est un maximum. Si f''(x) = 0, il faut utiliser d'autres méthodes.
  • Comment calculer la dérivée d'une fonction composée ?

    On utilise la règle de la chaîne : (f(g(x)))' = f'(g(x)) * g'(x)