Mathématiques > Analyse > Intégration > Propriétés de l'intégrale

Propriété de positivité de l'intégrale

Découvrez la propriété de positivité de l'intégrale définie, son importance et comment l'appliquer.

Introduction

La propriété de positivité de l'intégrale est une conséquence directe du lien entre l'intégrale et l'aire sous une courbe. Elle nous indique comment le signe de la fonction intégrée influence le signe de l'intégrale.

Énoncé de la Propriété

Si une fonction f(x) est continue et positive (ou nulle) sur un intervalle [a, b], c'est-à-dire f(x) ≥ 0 pour tout x dans [a, b], alors l'intégrale de f(x) sur cet intervalle est également positive (ou nulle) :

∫ab f(x) dx ≥ 0

De même, si f(x) est continue et négative (ou nulle) sur [a, b], c'est-à-dire f(x) ≤ 0 pour tout x dans [a, b], alors l'intégrale de f(x) sur cet intervalle est négative (ou nulle) :

∫ab f(x) dx ≤ 0

Interprétation Géométrique

L'intégrale d'une fonction positive représente l'aire sous la courbe de cette fonction et au-dessus de l'axe des abscisses. Puisque l'aire est une quantité positive (ou nulle), l'intégrale est également positive (ou nulle). De même, l'intégrale d'une fonction négative représente l'aire 'au-dessous' de l'axe des abscisses, et est donc considérée comme négative.

Conséquence: Comparaison d'intégrales

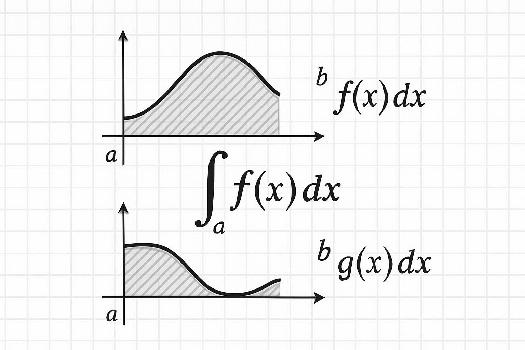
Une conséquence importante de la propriété de positivité est la possibilité de comparer des intégrales. Si f(x) ≥ g(x) pour tout x dans [a, b], alors :

∫ab f(x) dx ≥ ∫ab g(x) dx

Cela est dû au fait que f(x) - g(x) ≥ 0, donc ∫ab [f(x) - g(x)] dx ≥ 0, ce qui peut être réécrit comme ∫ab f(x) dx - ∫ab g(x) dx ≥ 0. Cela nous permet de déduire des inégalités entre les valeurs des intégrales basées sur la comparaison des fonctions intégrées.

Exemple

Considérons la fonction f(x) = x2 sur l'intervalle [0, 1]. Puisque x2 ≥ 0 pour tout x dans [0, 1], nous savons que ∫01 x2 dx ≥ 0. En fait, ∫01 x2 dx = [x3/3]01 = 1/3, ce qui est bien positif.

Ce qu'il faut retenir

  • Si f(x) ≥ 0 sur [a, b], alors ∫ab f(x) dx ≥ 0.
  • Si f(x) ≤ 0 sur [a, b], alors ∫ab f(x) dx ≤ 0.
  • Si f(x) ≥ g(x) sur [a, b], alors ∫ab f(x) dx ≥ ∫ab g(x) dx.
La propriété de positivité permet de déduire des inégalités entre les intégrales en se basant sur les inégalités entre les fonctions.

← Prolongement par continuité Règles de dérivation : Somme, Produit, Quotient, Composition →

FAQ

  • La propriété de positivité s'applique-t-elle si f(x) est positive sur une partie de l'intervalle et négative sur une autre partie ?

    Non, la propriété de positivité s'applique lorsque f(x) a un signe constant sur tout l'intervalle [a, b]. Si le signe de f(x) change, il faut diviser l'intégrale en sous-intervalles où f(x) a un signe constant et appliquer la propriété d'additivité.
  • Quelle est l'importance de la continuité de la fonction pour cette propriété ?

    La continuité de la fonction assure que l'intégrale existe et qu'elle représente bien l'aire sous la courbe. Bien que la propriété puisse parfois s'appliquer à des fonctions discontinues, la continuité est une condition suffisante pour sa validité.