Mathématiques > Géométrie > Trigonométrie > Cosinus, sinus et tangente d'un angle

Comprendre le Cosinus, le Sinus et la Tangente d'un Angle

Explorez en détail les concepts de cosinus, sinus et tangente dans un triangle rectangle. Apprenez à les calculer, à les utiliser pour résoudre des problèmes de géométrie et de trigonométrie, et découvrez leurs applications concrètes. Ce guide est conçu pour les élèves de lycée et propose des explications claires, des exemples variés et des exercices pratiques.

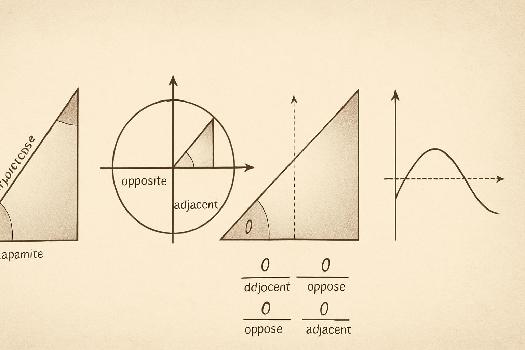
Introduction à la Trigonométrie et aux Angles

La trigonométrie est une branche essentielle des mathématiques qui étudie les relations entre les angles et les côtés des triangles. Elle est particulièrement utile dans l'étude des triangles rectangles. Les trois fonctions trigonométriques de base sont le cosinus, le sinus et la tangente. Avant de les aborder, rappelons quelques notions clés:

  • Triangle Rectangle : Un triangle avec un angle droit (90 degrés).
  • Hypoténuse : Le côté opposé à l'angle droit, c'est le côté le plus long du triangle rectangle.
  • Côté Adjacent : Le côté qui est adjacent à l'angle considéré (autre que l'hypoténuse).
  • Côté Opposé : Le côté opposé à l'angle considéré.

Définitions du Cosinus, Sinus et Tangente

Dans un triangle rectangle, pour un angle aigu donné (habituellement noté θ), on définit:

  • Cosinus (cos θ) : Le rapport entre la longueur du côté adjacent à l'angle θ et la longueur de l'hypoténuse. cos θ = Côté Adjacent / Hypoténuse
  • Sinus (sin θ) : Le rapport entre la longueur du côté opposé à l'angle θ et la longueur de l'hypoténuse. sin θ = Côté Opposé / Hypoténuse
  • Tangente (tan θ) : Le rapport entre la longueur du côté opposé à l'angle θ et la longueur du côté adjacent à l'angle θ. tan θ = Côté Opposé / Côté Adjacent. La tangente peut également être exprimée comme tan θ = sin θ / cos θ

Moyen mnémotechnique : SOH CAH TOA

Pour se souvenir facilement des définitions de sinus, cosinus et tangente, on utilise l'acronyme SOH CAH TOA:

  • SOH : Sinus = Opposé / Hypoténuse
  • CAH : Cosinus = Adjacent / Hypoténuse
  • TOA : Tangente = Opposé / Adjacent

Exemples de Calculs

Considérons un triangle rectangle ABC, avec un angle droit en B. Supposons que l'angle en A est θ, AB (côté adjacent) = 4, AC (hypoténuse) = 5, et BC (côté opposé) = 3.

  • cos θ = AB / AC = 4 / 5 = 0.8
  • sin θ = BC / AC = 3 / 5 = 0.6
  • tan θ = BC / AB = 3 / 4 = 0.75

Angles Remarquables et Valeurs Trigonométriques

Certains angles sont dits "remarquables" car leurs valeurs trigonométriques sont faciles à retenir et fréquemment utilisées. Ces angles sont 0°, 30°, 45°, 60° et 90°. Voici un tableau récapitulatif:

Angle (°) Angle (radians) sin θ cos θ tan θ
0 0 0 1 0
30 π/6 1/2 √3/2 √3/3
45 π/4 √2/2 √2/2 1
60 π/3 √3/2 1/2 √3
90 π/2 1 0 Non défini
Il est important de se familiariser avec ces valeurs.

Applications Pratiques

Les fonctions trigonométriques sont utilisées dans de nombreux domaines, notamment:

  • Navigation : Déterminer des distances et des directions.
  • Architecture : Calculer des angles et des longueurs pour la construction de bâtiments.
  • Physique : Étudier les mouvements ondulatoires et les oscillations.
  • Topographie : Mesurer des hauteurs et des distances sur le terrain.
Exemple : Un arbre est situé à une certaine distance d'un observateur. L'observateur mesure l'angle entre le sol et le sommet de l'arbre, qui est de 30°. Si l'observateur se trouve à 20 mètres de la base de l'arbre, quelle est la hauteur de l'arbre? Solution: On utilise la tangente: tan(30°) = hauteur / distance. Donc, hauteur = distance * tan(30°) = 20 * (√3/3) ≈ 11.55 mètres.

Ce qu'il faut retenir

  • Le cosinus d'un angle est le rapport du côté adjacent sur l'hypoténuse.
  • Le sinus d'un angle est le rapport du côté opposé sur l'hypoténuse.
  • La tangente d'un angle est le rapport du côté opposé sur le côté adjacent.
  • SOH CAH TOA est un moyen mnémotechnique pour se souvenir des définitions.
  • Connaître les valeurs trigonométriques des angles remarquables (0°, 30°, 45°, 60°, 90°) est essentiel.
  • Les fonctions trigonométriques ont de nombreuses applications pratiques dans divers domaines.

← Calcul des Volumes : Prisme, Cylindre, Pyramide, Cône et Sphère Distance d'un Point à une Droite et d'un Point à un Plan →

FAQ

  • Comment trouver l'angle si je connais le cosinus, le sinus ou la tangente?

    Vous pouvez utiliser les fonctions trigonométriques inverses (arccosinus, arcsinus, arctangente), souvent notées cos-1, sin-1, tan-1 ou acos, asin, atan sur les calculatrices. Par exemple, si cos θ = 0.5, alors θ = cos-1(0.5) = 60°.
  • La tangente peut-elle être indéfinie?

    Oui, la tangente est indéfinie lorsque l'angle est de 90° (π/2 radians) car le côté adjacent est nul, et la division par zéro n'est pas définie.