Mathématiques > Géométrie > Géométrie Spatiale > Orthogonalité de droites et de plans

Orthogonalité de Droites et de Plans dans l'Espace

Explorez en détail l'orthogonalité entre droites et plans, un concept fondamental de la géométrie spatiale. Ce guide complet, conçu pour les élèves de lycée, vous fournira les définitions, les propriétés et les méthodes nécessaires pour maîtriser ce sujet.

Définitions préliminaires

Avant d'aborder l'orthogonalité, rappelons quelques définitions essentielles :

  • Droite : Une ligne infinie définie par deux points distincts.
  • Plan : Une surface infinie et plate définie par trois points non alignés, ou par une droite et un point extérieur à cette droite.
  • Vecteur directeur d'une droite : Un vecteur non nul qui indique la direction de la droite.
  • Vecteur normal d'un plan : Un vecteur non nul orthogonal à tous les vecteurs contenus dans le plan.
Ces notions sont cruciales pour comprendre l'orthogonalité.

Orthogonalité d'une droite et d'un plan

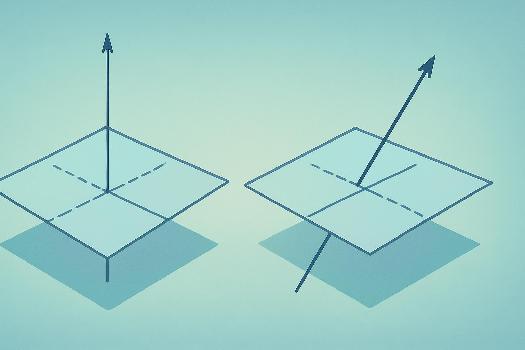
Une droite (d) est dite orthogonale à un plan (P) si elle est perpendiculaire à toutes les droites contenues dans ce plan et passant par son point d'intersection avec (P). En pratique, il suffit de montrer que (d) est perpendiculaire à deux droites sécantes de (P). Critère d'orthogonalité : Une droite (d) de vecteur directeur u est orthogonale à un plan (P) si et seulement si u est colinéaire à un vecteur normal n de (P), c'est-à-dire s'il existe un réel k tel que u = kn. Exemple : Considérons un plan (P) d'équation ax + by + cz + d = 0 et une droite (d) passant par un point A(x0, y0, z0) et de vecteur directeur u(l, m, n). La droite (d) est orthogonale à (P) si et seulement si le vecteur normal de (P), n(a, b, c), est colinéaire à u. Cela signifie que a/l = b/m = c/n.

Comment démontrer l'orthogonalité d'une droite et d'un plan?

Voici les étapes à suivre pour démontrer que une droite est orthogonale à un plan :

  1. Identifier le vecteur directeur u de la droite (d).
  2. Identifier le vecteur normal n du plan (P). Si l'équation du plan est donnée sous la forme ax + by + cz + d = 0, alors n(a, b, c).
  3. Vérifier si les vecteurs u et n sont colinéaires. On peut le faire en vérifiant si leurs coordonnées sont proportionnelles (a/l = b/m = c/n) ou en montrant que u = kn pour un certain réel k.
  4. Conclusion : Si les vecteurs sont colinéaires, alors la droite (d) est orthogonale au plan (P).
Exemple : Soit le plan (P) d'équation 2x - y + 3z - 5 = 0 et la droite (d) passant par le point A(1, 2, 3) et de vecteur directeur u(2, -1, 3). Le vecteur normal de (P) est n(2, -1, 3). Comme u = n, alors la droite (d) est orthogonale au plan (P).

Propriétés importantes

  • Si une droite est orthogonale à un plan, alors elle est orthogonale à toute droite contenue dans ce plan.
  • Si deux plans sont parallèles, toute droite orthogonale à l'un est orthogonale à l'autre.
  • Si deux droites sont parallèles, tout plan orthogonal à l'une est orthogonal à l'autre.

Applications

L'orthogonalité des droites et des plans trouve des applications dans divers domaines :

  • Architecture : Pour s'assurer de la stabilité et de la perpendicularité des structures.
  • Construction : Pour aligner correctement les éléments de construction.
  • Infographie : Pour la modélisation 3D et le rendu d'images réalistes.
  • Physique : Pour l'étude des forces et des champs.

Ce qu'il faut retenir

  • Une droite (d) est orthogonale à un plan (P) si elle est perpendiculaire à toutes les droites de (P) passant par leur point d'intersection.
  • Il suffit de montrer que (d) est perpendiculaire à deux droites sécantes de (P) pour prouver l'orthogonalité.
  • Une droite (d) de vecteur directeur u est orthogonale à un plan (P) de vecteur normal n si et seulement si u et n sont colinéaires.
  • Pour démontrer l'orthogonalité, identifier u et n, puis vérifier leur colinéarité.
  • Si une droite est orthogonale à un plan, elle est orthogonale à toute droite contenue dans ce plan.

← Orthogonalité de Deux Droites dans l'Espace Orthogonalité et Applications Avancées du Produit Scalaire dans l'Espace →

FAQ

  • Comment vérifier rapidement si une droite est orthogonale à un plan ?

    Vérifiez si le vecteur directeur de la droite est colinéaire au vecteur normal du plan. Si c'est le cas, la droite est orthogonale au plan.
  • Est-ce que toute droite perpendiculaire à une droite d'un plan est orthogonale à ce plan ?

    Non, une droite doit être perpendiculaire à deux droites sécantes du plan pour être orthogonale à ce plan. Être perpendiculaire à une seule droite ne suffit pas.
  • Comment trouver le vecteur normal d'un plan à partir de son équation cartésienne ?

    Si l'équation du plan est de la forme ax + by + cz + d = 0, alors le vecteur normal est n(a, b, c).