Transformations Géométriques avec les Nombres Complexes

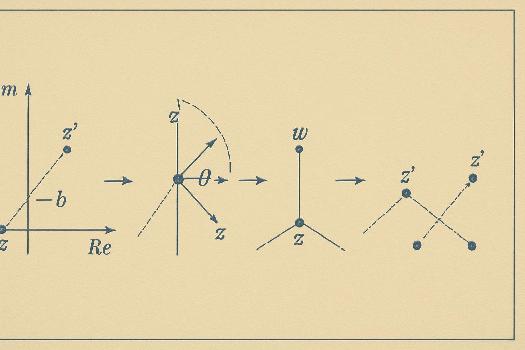
Introduction aux Transformations et Nombres Complexes

Bienvenue dans le monde fascinant des transformations géométriques et des nombres complexes ! Dans ce cours, nous allons explorer comment les nombres complexes peuvent être utilisés pour représenter et manipuler des transformations géométriques telles que les translations, les rotations et les homothéties. Les nombres complexes offrent une manière élégante et efficace de décrire ces transformations, simplifiant ainsi les calculs et les visualisations.

Translation

Une translation est un déplacement de tous les points d'une figure dans la même direction et sur la même distance. En termes de nombres complexes, une translation est représentée par l'addition d'un nombre complexe constant. Si un point M a pour affixe z, et que l'on applique une translation de vecteur d'affixe b, alors l'image M' de M a pour affixe z' telle que :

z' = z + b

Exemple : Soit le point M d'affixe z = 2 + 3i. Si on lui applique une translation de vecteur d'affixe b = 1 - i, alors l'affixe de l'image M' est :

z' = (2 + 3i) + (1 - i) = 3 + 2i

Rotation

Une rotation est une transformation qui fait tourner une figure autour d'un point fixe (le centre de rotation) d'un certain angle. Si un point M a pour affixe z, et que l'on applique une rotation de centre ω (d'affixe ω) et d'angle θ, alors l'image M' de M a pour affixe z' telle que :

z' - ω = e^iθ(z - ω)

Ou encore :

z' = ω + e^iθ(z - ω)

Où e^iθ = cos(θ) + i sin(θ) est la notation exponentielle d'un nombre complexe de module 1 et d'argument θ.

Exemple : Soit le point M d'affixe z = 1 + i. Si on lui applique une rotation de centre Ω d'affixe ω = 2 et d'angle θ = π/2, alors :

z' = 2 + e^iπ/2(1 + i - 2) = 2 + i(-1 + i) = 2 - i - 1 = 1 - i

Homothétie

Une homothétie est une transformation qui agrandit ou réduit une figure par un facteur constant (le rapport d'homothétie) par rapport à un point fixe (le centre d'homothétie). Si un point M a pour affixe z, et que l'on applique une homothétie de centre ω (d'affixe ω) et de rapport k, alors l'image M' de M a pour affixe z' telle que :

z' - ω = k(z - ω)

Ou encore :

z' = ω + k(z - ω)

Exemple : Soit le point M d'affixe z = 3 + i. Si on lui applique une homothétie de centre Ω d'affixe ω = 1 et de rapport k = 2, alors :

z' = 1 + 2(3 + i - 1) = 1 + 2(2 + i) = 1 + 4 + 2i = 5 + 2i

Combinaison de Transformations

Il est possible de combiner plusieurs transformations géométriques. L'application successive de transformations se traduit par une composition des expressions complexes correspondantes. Il faut faire attention à l'ordre d'application des transformations, car en général la composition n'est pas commutative. Par exemple, appliquer une rotation suivie d'une translation n'est pas la même chose que d'appliquer une translation suivie d'une rotation.

Ce qu'il faut retenir

• Translation : z' = z + b, où b est l'affixe du vecteur de translation.
• Rotation : z' = ω + e^iθ(z - ω), où ω est l'affixe du centre de rotation et θ est l'angle de rotation. e^iθ = cos(θ) + i sin(θ)
• Homothétie : z' = ω + k(z - ω), où ω est l'affixe du centre d'homothétie et k est le rapport d'homothétie.
• La composition de transformations se traduit par la composition des expressions complexes correspondantes.