Mathématiques > Géométrie > Géométrie Plane > Distance entre deux points

Distance entre deux points dans un repère orthonormé

Apprenez à calculer la distance entre deux points dans un repère orthonormé, un concept fondamental en géométrie plane. Ce cours complet, avec exemples et exercices, est spécialement conçu pour les élèves de lycée.

Introduction à la distance entre deux points

En géométrie plane, la distance entre deux points est la longueur du segment de droite qui les relie. Comprendre comment calculer cette distance est essentiel pour résoudre de nombreux problèmes géométriques. Nous allons utiliser le repère orthonormé, un système de coordonnées dans lequel les axes sont perpendiculaires et les unités de longueur sont égales.

Le repère orthonormé

Un repère orthonormé est défini par deux axes perpendiculaires, généralement appelés l'axe des abscisses (axe des x) et l'axe des ordonnées (axe des y). Chaque point dans le plan peut être identifié par ses coordonnées (x, y), où x est l'abscisse et y est l'ordonnée.

L'origine du repère, notée O, a pour coordonnées (0, 0).

Repère orthonormé

Formule de la distance entre deux points

Soient A(xA, yA) et B(xB, yB) deux points dans un repère orthonormé. La distance entre A et B, notée AB, est donnée par la formule suivante :

AB = √((xB - xA)2 + (yB - yA)2)

Cette formule est une application directe du théorème de Pythagore.

Démonstration de la formule

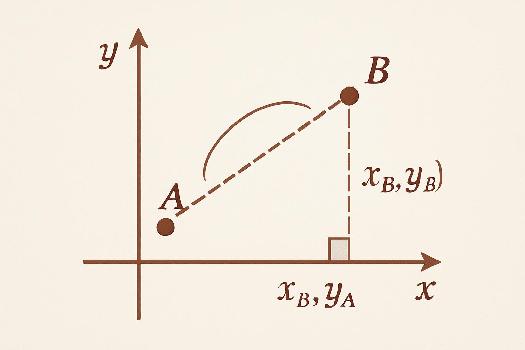
Considérons le triangle rectangle ABC, où C est le point de coordonnées (xB, yA). La longueur du côté AC est |xB - xA| et la longueur du côté BC est |yB - yA|.

D'après le théorème de Pythagore :

AB2 = AC2 + BC2

AB2 = (xB - xA)2 + (yB - yA)2

AB = √((xB - xA)2 + (yB - yA)2)

Exemples d'application

Exemple 1: Calculer la distance entre les points A(1, 2) et B(4, 6).

AB = √((4 - 1)2 + (6 - 2)2)

AB = √(32 + 42)

AB = √(9 + 16)

AB = √25

AB = 5

Exemple 2: Calculer la distance entre les points C(-2, 3) et D(1, -1).

CD = √((1 - (-2))2 + (-1 - 3)2)

CD = √(32 + (-4)2)

CD = √(9 + 16)

CD = √25

CD = 5

Cas particuliers

  • Points sur la même horizontale : Si yA = yB, alors AB = |xB - xA|.
  • Points sur la même verticale : Si xA = xB, alors AB = |yB - yA|.

Exercices

Exercice 1: Calculer la distance entre les points E(0, 0) et F(3, 4).

Exercice 2: Calculer la distance entre les points G(-1, -2) et H(2, 2).

Exercice 3: Les points I(1, 1), J(5, 4) et K(8, 0) forment-ils un triangle rectangle? (Indice: Utilisez le théorème de Pythagore.)

Ce qu'il faut retenir

  • La distance entre deux points A(xA, yA) et B(xB, yB) dans un repère orthonormé est donnée par la formule : AB = √((xB - xA)2 + (yB - yA)2).
  • Cette formule découle du théorème de Pythagore.
  • Si les points sont sur la même horizontale, AB = |xB - xA|.
  • Si les points sont sur la même verticale, AB = |yB - yA|.

← Distance d'un Point à une Droite et d'un Point à un Plan Droites et plans dans l'espace : équations paramétriques et cartésiennes →

FAQ

  • Comment simplifier le calcul de la distance si les points ont la même abscisse ou la même ordonnée?

    Si les points ont la même abscisse, la distance est la valeur absolue de la différence de leurs ordonnées. Si les points ont la même ordonnée, la distance est la valeur absolue de la différence de leurs abscisses.
  • La distance entre deux points peut-elle être négative?

    Non, la distance est toujours une valeur positive ou nulle. Elle représente une longueur.