Mathématiques > Géométrie > Géométrie Spatiale > Produit scalaire dans l'espace

Orthogonalité et Applications Avancées du Produit Scalaire dans l'Espace

Approfondissez votre compréhension du produit scalaire en explorant l'orthogonalité des vecteurs et ses applications avancées. Ce cours présente des techniques de résolution de problèmes et des exemples complexes, idéaux pour les élèves de lycée souhaitant maîtriser ce concept.

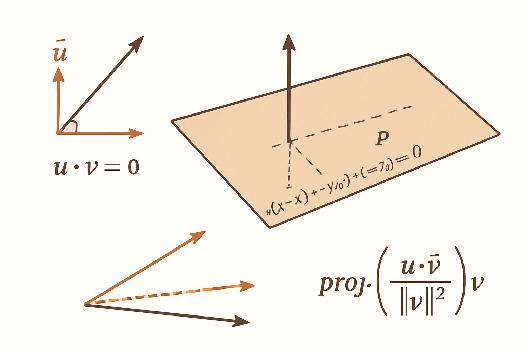
Orthogonalité des Vecteurs

Deux vecteurs u et v sont dits orthogonaux (ou perpendiculaires) si et seulement si leur produit scalaire est nul, c'est-à-dire u · v = 0. Cette condition est équivalente à dire que l'angle θ entre u et v est de 90 degrés (π/2 radians), car cos(π/2) = 0.

Exemple: Les vecteurs u = (1, -1, 0) et v = (1, 1, 2) sont-ils orthogonaux?
Solution: u · v = (1)(1) + (-1)(1) + (0)(2) = 1 - 1 + 0 = 0. Oui, ils sont orthogonaux.

Applications à la Géométrie Analytique

Le produit scalaire est un outil puissant pour résoudre des problèmes en géométrie analytique, notamment pour trouver des équations de plans et de droites.

  • Équation d'un plan: Un plan peut être défini par un point A(x₀, y₀, z₀) appartenant au plan et un vecteur normal n = (a, b, c) au plan. Un point M(x, y, z) appartient au plan si et seulement si AM · n = 0, où AM = (x - x₀, y - y₀, z - z₀). Ainsi, l'équation du plan est a(x - x₀) + b(y - y₀) + c(z - z₀) = 0.
  • Distance d'un point à un plan: La distance d'un point P(x₁, y₁, z₁) au plan d'équation ax + by + cz + d = 0 est donnée par la formule: |ax₁ + by₁ + cz₁ + d| / √(a² + b² + c²).

Projections Orthogonales

La projection orthogonale d'un vecteur u sur un vecteur non nul v est le vecteur projvu = (u · v / ||v||²) * v. Ce vecteur est parallèle à v et représente la composante de u qui est dans la direction de v.

Exemple: Trouver la projection de u = (3, 4, 0) sur v = (1, 0, 0).
Solution: u · v = (3)(1) + (4)(0) + (0)(0) = 3. ||v||² = 1² + 0² + 0² = 1. Donc, projvu = (3/1) * (1, 0, 0) = (3, 0, 0).

Exemple Avancé

Soit le plan P d'équation x + 2y - z + 3 = 0 et le point A(1, 1, 1). Calculer la distance du point A au plan P.
Solution: En utilisant la formule de la distance d'un point à un plan, on a:
Distance = |(1)(1) + (2)(1) + (-1)(1) + 3| / √(1² + 2² + (-1)²) = |1 + 2 - 1 + 3| / √(1 + 4 + 1) = 5 / √6 = (5√6) / 6.

Ce qu'il faut retenir

  • Orthogonalité: u · v = 0 ⇔ u et v sont orthogonaux.
  • Équation d'un plan: a(x - x₀) + b(y - y₀) + c(z - z₀) = 0 (avec vecteur normal (a,b,c)).
  • Distance point-plan: |ax₁ + by₁ + cz₁ + d| / √(a² + b² + c²).
  • Projection orthogonale: projvu = (u · v / ||v||²) * v.

← Orthogonalité de Droites et de Plans dans l'Espace Relations Trigonométriques Fondamentales : Un Guide Détaillé →

FAQ

  • Comment trouver un vecteur normal à un plan?

    Les coefficients x, y, et z de l'équation du plan ax + by + cz + d = 0 forment un vecteur normal au plan, soit (a, b, c).
  • Est-ce que deux plans sont parallèles si leurs vecteurs normaux sont colinéaires?

    Oui, deux plans sont parallèles si et seulement si leurs vecteurs normaux sont colinéaires (c'est-à-dire, multiples l'un de l'autre).
  • Comment utiliser le produit scalaire pour déterminer l'équation d'une droite perpendiculaire à un plan et passant par un point donné?

    Le vecteur directeur de la droite est le vecteur normal du plan. Utilisez ce vecteur directeur et les coordonnées du point pour écrire l'équation paramétrique de la droite.