Mathématiques > Nombres Complexes (Terminale) > Forme Trigonométrique et Exponentielle > Argument d'un nombre complexe

Argument d'un Nombre Complexe : Définition et Calcul

Découvrez l'argument d'un nombre complexe, sa définition, comment le calculer et son importance dans la représentation trigonométrique et exponentielle. Ce guide complet, avec des exemples détaillés, est parfait pour les élèves de Terminale.

Définition de l'Argument

L'argument d'un nombre complexe non nul z, noté arg(z), est une mesure, en radians, de l'angle orienté entre l'axe des réels (l'axe des abscisses) et le vecteur représentant z dans le plan complexe. Il est important de noter que l'argument n'est pas unique. Si θ est un argument de z, alors θ + 2kπ, où k est un entier relatif, est également un argument de z. On parle d'argument principal lorsqu'on choisit l'argument dans l'intervalle ]-π, π].

Représentation Graphique

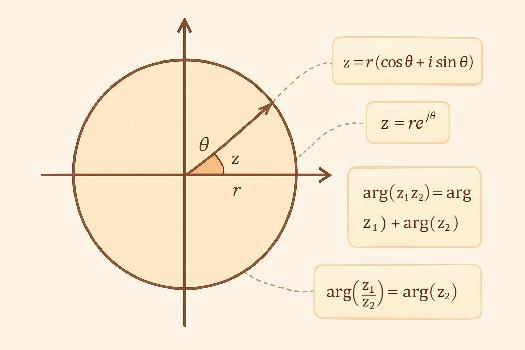
Imaginez le plan complexe. Un nombre complexe z = a + bi est représenté par un point M de coordonnées (a, b). L'argument de z est l'angle que forme la demi-droite [Ox) avec la demi-droite [OM). Visualiser l'argument sur un graphique aide à comprendre sa signification géométrique.

Calcul de l'Argument

Pour calculer l'argument d'un nombre complexe z = a + bi, on utilise les fonctions trigonométriques. On a :

  • cos(θ) = a / |z|
  • sin(θ) = b / |z|
Où |z| est le module de z, calculé comme |z| = √(a2 + b2). On peut donc trouver θ en utilisant les fonctions arccos ou arcsin. Cependant, il est crucial de considérer le signe de a et b pour déterminer le quadrant dans lequel se trouve l'argument, et ainsi choisir la bonne valeur de θ. La fonction atan2(b, a) est particulièrement utile car elle prend en compte les signes de a et b pour renvoyer l'argument correct dans l'intervalle ]-π, π].

Exemple 1: z = 1 + i

Calculons l'argument de z = 1 + i. On a a = 1 et b = 1. Le module est |z| = √(12 + 12) = √2. Donc, cos(θ) = 1/√2 et sin(θ) = 1/√2. L'argument principal est θ = π/4.

Exemple 2: z = -1 + i

Calculons l'argument de z = -1 + i. On a a = -1 et b = 1. Le module est |z| = √((-1)2 + 12) = √2. Donc, cos(θ) = -1/√2 et sin(θ) = 1/√2. L'argument principal est θ = 3π/4.

Argument et Forme Trigonométrique

Si z a pour module r et pour argument θ, alors z peut s'écrire sous forme trigonométrique: z = r(cos(θ) + i sin(θ)). Cette forme est très utile pour les multiplications et divisions de nombres complexes.

Argument et Forme Exponentielle

La forme exponentielle d'un nombre complexe z est donnée par z = r eiθ, où r est le module de z et θ est un argument de z. La formule d'Euler relie les fonctions exponentielles et trigonométriques: eiθ = cos(θ) + i sin(θ). La forme exponentielle simplifie considérablement les calculs impliquant des puissances et des racines de nombres complexes.

Propriétés de l'Argument

L'argument possède plusieurs propriétés importantes:

  • arg(z1 * z2) = arg(z1) + arg(z2) (modulo 2π)
  • arg(z1 / z2) = arg(z1) - arg(z2) (modulo 2π)
  • arg(zn) = n arg(z) (modulo 2π)
  • arg(z) = -arg(z*) où z* est le conjugué de z.
Ces propriétés sont essentielles pour simplifier les calculs et résoudre des équations complexes.

Ce qu'il faut retenir

  • L'argument d'un nombre complexe z est l'angle orienté entre l'axe réel et le vecteur représentant z.
  • L'argument n'est pas unique, il est défini à 2kπ près. L'argument principal appartient à l'intervalle ]-π, π].
  • Pour calculer l'argument de z = a + bi, on utilise les relations cos(θ) = a / |z| et sin(θ) = b / |z|.
  • La forme trigonométrique de z est z = r(cos(θ) + i sin(θ)), où r est le module et θ est un argument.
  • La forme exponentielle de z est z = r eiθ.
  • arg(z1 * z2) = arg(z1) + arg(z2) (modulo 2π)
  • arg(z1 / z2) = arg(z1) - arg(z2) (modulo 2π)

← Applications Géométriques des Nombres Complexes: Transformations et Lieux Conjugué et Module d'un Nombre Complexe : Guide Complet →

FAQ

  • Comment trouver l'argument principal d'un nombre complexe ?

    Après avoir calculé un argument θ, ajoutez ou soustrayez des multiples de 2π jusqu'à ce que la valeur de θ se trouve dans l'intervalle ]-π, π].
  • Pourquoi l'argument d'un nombre complexe est-il important ?

    L'argument est crucial pour la représentation trigonométrique et exponentielle des nombres complexes, ce qui facilite grandement les opérations de multiplication, division et élévation à la puissance.
  • Que se passe-t-il si le nombre complexe est nul ?

    Le nombre complexe 0 n'a pas d'argument défini.