Applications Géométriques des Nombres Complexes: Transformations et Lieux

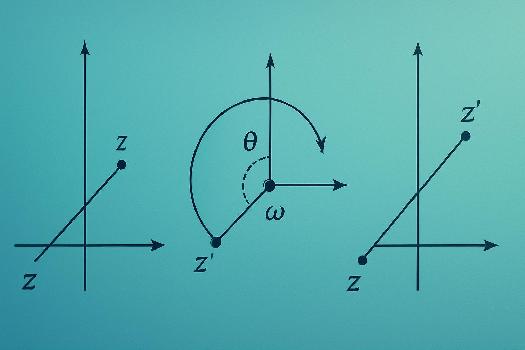
Rappel: Représentation Géométrique

Tout nombre complexe z = a + bi peut être associé à un point M de coordonnées (a, b) dans le plan complexe, appelé le plan d'Argand-Cauchy. L'axe des abscisses représente les nombres réels (axe réel) et l'axe des ordonnées représente les nombres imaginaires purs (axe imaginaire). Le module de z, noté |z|, est la distance OM. L'argument de z, noté arg(z), est l'angle (Ox, OM), où Ox est l'axe réel.

Translations

Une translation de vecteur u d'affixe t transforme un point M d'affixe z en un point M' d'affixe z' telle que z' = z + t. Géométriquement, cela signifie que le vecteur MM' est égal au vecteur u. Exemple: Si on translate le point M d'affixe 2 + i par le vecteur d'affixe 1 - 3i, on obtient le point M' d'affixe (2 + i) + (1 - 3i) = 3 - 2i.

Rotations

Une rotation de centre Ω d'affixe ω et d'angle θ transforme un point M d'affixe z en un point M' d'affixe z' telle que z' - ω = e^iθ(z - ω). Ceci signifie que la distance ΩM est égale à la distance ΩM' et que l'angle (ΩM, ΩM') est égal à θ. Exemple: Une rotation de centre O (origine) et d'angle π/2 transforme le point M d'affixe 1 + i en un point M' d'affixe e^iπ/2(1 + i) = i(1 + i) = i - 1 = -1 + i.

Homothéties

Une homothétie de centre Ω d'affixe ω et de rapport k (k réel) transforme un point M d'affixe z en un point M' d'affixe z' telle que z' - ω = k(z - ω). Cela signifie que les points Ω, M et M' sont alignés et que la distance ΩM' est égale à |k| fois la distance ΩM. Exemple: Une homothétie de centre O et de rapport 2 transforme le point M d'affixe 1 + i en un point M' d'affixe 2(1 + i) = 2 + 2i.

Similitudes Directes

Une similitude directe est une transformation qui combine une rotation et une homothétie de même centre. Elle transforme un point M d'affixe z en un point M' d'affixe z' telle que z' = az + b, où a et b sont des nombres complexes et a ≠ 0. Le rapport de la similitude est |a| et l'angle est arg(a). Le centre Ω d'affixe ω est le point invariant de la transformation, tel que ω = aω + b, donc ω = b / (1 - a) (si a ≠ 1). Si a=1 il s'agit d'une translation.

Détermination de Lieux Géométriques

Les nombres complexes sont très utiles pour déterminer des lieux géométriques. Pour cela, on exprime l'affixe z d'un point M en fonction de certaines conditions (par exemple, une relation entre z et z', où z' est l'affixe d'un autre point M' lié à M par une transformation). On cherche ensuite une équation en x et y (où z = x + iy) qui représente le lieu géométrique. Exemple: On considère la transformation z' = (1 + i)z. Si M décrit un cercle de centre O et de rayon 1, alors |z| = 1. On a |z'| = |(1 + i)z| = |1 + i||z| = √2 * 1 = √2. Donc, M' décrit un cercle de centre O et de rayon √2.

Ce qu'il faut retenir

• Une translation d'affixe t transforme z en z' = z + t.
• Une rotation de centre ω et d'angle θ transforme z en z' - ω = e^iθ(z - ω).
• Une homothétie de centre ω et de rapport k transforme z en z' - ω = k(z - ω).
• Une similitude directe transforme z en z' = az + b.
• Les nombres complexes sont utilisés pour déterminer des lieux géométriques en exprimant les conditions géométriques en termes d'équations complexes.