Mathématiques > Nombres Complexes (Terminale) > Introduction aux Nombres Complexes > Division de nombres complexes

Division des nombres complexes

Apprenez à diviser les nombres complexes étape par étape. Ce cours détaille la méthode avec des exemples pour faciliter la compréhension en Terminale.

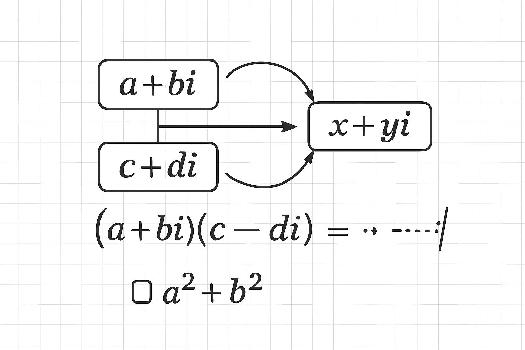
Introduction à la division des nombres complexes

La division des nombres complexes est une opération qui peut sembler complexe au premier abord, mais qui repose sur une idée simple : se débarrasser de la partie imaginaire au dénominateur. Pour ce faire, on utilise le conjugué du dénominateur. Rappelons qu'un nombre complexe se présente sous la forme z = a + bi, où a est la partie réelle et b la partie imaginaire. Le conjugué de z, noté z̄, est alors z̄ = a - bi. Le produit d'un nombre complexe par son conjugué donne un nombre réel : z * z̄ = (a + bi)(a - bi) = a2 + b2.

Méthode de division

Pour diviser deux nombres complexes, disons z1 = a + bi et z2 = c + di, on procède comme suit :

  1. Écrire la division sous forme de fraction : z1 / z2 = (a + bi) / (c + di).
  2. Multiplier le numérateur et le dénominateur par le conjugué du dénominateur : [(a + bi) * (c - di)] / [(c + di) * (c - di)].
  3. Développer et simplifier le numérateur et le dénominateur. Rappelez-vous que i2 = -1.
  4. Écrire le résultat sous la forme x + yi, où x est la partie réelle et y la partie imaginaire.

Exemple 1

Divisons z1 = 3 + 4i par z2 = 1 - 2i.

  1. On écrit la fraction : (3 + 4i) / (1 - 2i).
  2. On multiplie par le conjugué du dénominateur (qui est 1 + 2i) : [(3 + 4i)(1 + 2i)] / [(1 - 2i)(1 + 2i)].
  3. On développe le numérateur : 3 + 6i + 4i + 8i2 = 3 + 10i - 8 = -5 + 10i.
  4. On développe le dénominateur : 1 + 2i - 2i - 4i2 = 1 + 4 = 5.
  5. On simplifie : (-5 + 10i) / 5 = -1 + 2i.
Donc, (3 + 4i) / (1 - 2i) = -1 + 2i.

Exemple 2

Divisons z1 = 2 - i par z2 = 3 + i.

  1. On écrit la fraction : (2 - i) / (3 + i).
  2. On multiplie par le conjugué du dénominateur (qui est 3 - i) : [(2 - i)(3 - i)] / [(3 + i)(3 - i)].
  3. On développe le numérateur : 6 - 2i - 3i + i2 = 6 - 5i - 1 = 5 - 5i.
  4. On développe le dénominateur : 9 - 3i + 3i - i2 = 9 + 1 = 10.
  5. On simplifie : (5 - 5i) / 10 = 1/2 - 1/2 i.
Donc, (2 - i) / (3 + i) = 1/2 - 1/2 i.

Astuces et Précautions

  • Toujours multiplier par le conjugué du dénominateur. C'est crucial!
  • Faites attention aux signes, surtout avec les i2.
  • Simplifiez au maximum votre résultat final.

Ce qu'il faut retenir

  • La division de nombres complexes nécessite de multiplier le numérateur et le dénominateur par le conjugué du dénominateur.
  • Le conjugué de a + bi est a - bi.
  • (a + bi)(a - bi) = a2 + b2, un nombre réel.
  • Après multiplication et simplification, le résultat doit être exprimé sous la forme x + yi.

← Conjugué et Module d'un Nombre Complexe : Guide Complet Exercices Corrigés : Transformations et Nombres Complexes →

FAQ

  • Pourquoi multiplie-t-on par le conjugué du dénominateur ?

    Multiplier par le conjugué du dénominateur permet d'éliminer la partie imaginaire au dénominateur, ce qui rend la fraction plus simple à manipuler et à exprimer sous la forme a + bi.
  • Que se passe-t-il si le dénominateur est un nombre réel ?

    Si le dénominateur est un nombre réel, la division est plus simple. Il suffit de diviser la partie réelle et la partie imaginaire du numérateur par ce nombre réel.
  • Peut-on diviser un nombre complexe par zéro ?

    Non, la division par zéro n'est pas définie dans l'ensemble des nombres complexes, tout comme dans l'ensemble des nombres réels.