Transformations du plan : Translations, Rotations, Symétries

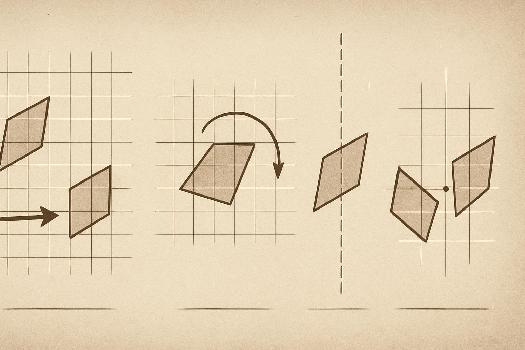
Introduction aux transformations

Les transformations géométriques sont des opérations qui modifient la position, la taille ou la forme d'une figure. Dans ce chapitre, nous allons explorer trois transformations fondamentales : les translations, les rotations et les symétries. Ces transformations sont essentielles en géométrie et trouvent de nombreuses applications dans d'autres domaines comme l'infographie, la physique et l'ingénierie. Important : Ces transformations conservent les distances (isométries).

Translations

Une translation est un déplacement de tous les points d'une figure dans la même direction et sur la même distance. Elle est définie par un vecteur.

Définition: Une translation de vecteur $\backslash vec\{u\}$ transforme un point A en un point A' tel que $\backslash vec\{AA\text{'}\}\; =\; \backslash vec\{u\}$.

Propriétés :

• Une translation conserve les distances et les angles.
• Une translation transforme une droite en une droite parallèle.
• L'image d'un segment par une translation est un segment de même longueur.

Exemple: Imaginez une flèche. La translation consiste à déplacer cette flèche sans la faire tourner ni la déformer.

Rotations

Une rotation est une transformation qui fait tourner une figure autour d'un point fixe, appelé centre de rotation. Elle est définie par un centre et un angle.

Définition: Une rotation de centre O et d'angle α transforme un point A en un point A' tel que OA = OA' et l'angle $\backslash angle\; AOA\text{'}\; =\; \backslash alpha$.

Propriétés:

• Une rotation conserve les distances et les angles.
• Une rotation transforme un cercle en un cercle de même rayon.
• L'image d'un segment par une rotation est un segment de même longueur.

Exemple: Imaginez une aiguille d'horloge qui tourne autour du centre de l'horloge. C'est une rotation.

Symétries

Il existe deux types de symétries : la symétrie axiale (ou réflexion) et la symétrie centrale.

Symétrie Axiale: Une symétrie axiale est une réflexion d'une figure par rapport à une droite, appelée axe de symétrie.

Définition: La symétrie axiale par rapport à une droite (d) transforme un point A en un point A' tel que (d) est la médiatrice du segment [AA'].

Propriétés:

• Une symétrie axiale conserve les distances et les angles.
• Une symétrie axiale transforme une droite en une droite.

Exemple: Imaginez un papillon. Ses deux ailes sont symétriques par rapport à un axe vertical.

Symétrie Centrale: Une symétrie centrale est une réflexion d'une figure par rapport à un point, appelé centre de symétrie.

Définition: La symétrie centrale par rapport à un point O transforme un point A en un point A' tel que O est le milieu du segment [AA'].

Propriétés:

• Une symétrie centrale conserve les distances et les angles.
• Une symétrie centrale transforme une droite en une droite parallèle.

Exemple: Imaginez un cercle et son centre. Chaque point du cercle a un point symétrique par rapport au centre.

Composition de transformations

Il est possible de combiner plusieurs transformations. Par exemple, on peut effectuer une translation suivie d'une rotation. L'ordre dans lequel on effectue les transformations est important, car il peut affecter le résultat final. La composition de deux translations est une translation. La composition de deux rotations de même centre est une rotation. La composition de deux symétries axiales d'axes parallèles est une translation.

Applications des transformations

Les transformations géométriques ont de nombreuses applications :

• Infographie: Création d'images, d'animations et de jeux vidéo.
• Physique: Étude des mouvements et des symétries des objets.
• Ingénierie: Conception de structures et de machines.
• Art: Création de motifs et de dessins symétriques.
• Cryptographie: Utilisation des transformations pour coder et décoder des messages.

Ce qu'il faut retenir

• Translation: Déplacement d'une figure dans une direction et sur une distance donnée par un vecteur.
• Rotation: Rotation d'une figure autour d'un point fixe (centre) d'un angle donné.
• Symétrie Axiale: Réflexion d'une figure par rapport à une droite (axe de symétrie).
• Symétrie Centrale: Réflexion d'une figure par rapport à un point (centre de symétrie).
• Les transformations conservent les distances (isométries) et les angles.
• La composition de transformations peut être utilisée pour créer des effets complexes.