Mathématiques > Algèbre > Fonctions > Sens de variation et extrema d'une fonction

Analyse des variations d'une fonction et identification des extrema

Comprenez comment déterminer le sens de variation d'une fonction à partir de sa dérivée, et comment identifier et classifier les extrema (maximums et minimums) locaux et globaux. Ce guide, avec des exemples détaillés, est parfait pour les lycéens.

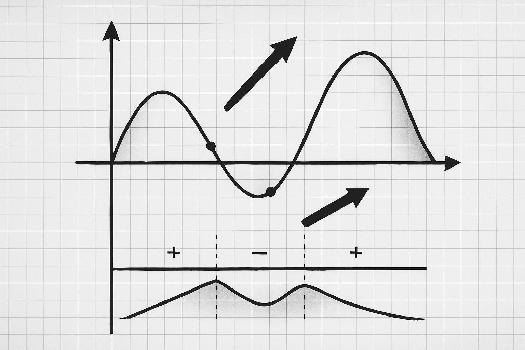
Introduction au sens de variation d'une fonction

Bienvenue dans ce guide complet sur le sens de variation des fonctions et la détermination des extrema! Comprendre comment une fonction augmente ou diminue est fondamental en mathématiques. Cela nous permet de résoudre des problèmes d'optimisation, de modéliser des phénomènes réels et de visualiser le comportement des fonctions. Nous allons explorer les concepts clés, les méthodes et les exemples pour vous aider à maîtriser cette notion essentielle. Nous allons utiliser la dérivée d'une fonction comme outil principal pour analyser son sens de variation.

Définition du sens de variation

Une fonction f est dite:

  • Croissante sur un intervalle I si, pour tout x1 et x2 dans I tels que x1 < x2, on a f(x1) ≤ f(x2).
  • Strictement croissante sur un intervalle I si, pour tout x1 et x2 dans I tels que x1 < x2, on a f(x1) < f(x2).
  • Décroissante sur un intervalle I si, pour tout x1 et x2 dans I tels que x1 < x2, on a f(x1) ≥ f(x2).
  • Strictement décroissante sur un intervalle I si, pour tout x1 et x2 dans I tels que x1 < x2, on a f(x1) > f(x2).
  • Constante sur un intervalle I si, pour tout x1 et x2 dans I, on a f(x1) = f(x2).
En d'autres termes, une fonction croissante monte quand on se déplace de gauche à droite sur son graphe, une fonction décroissante descend, et une fonction constante reste à la même hauteur.

La dérivée et le sens de variation

La dérivée d'une fonction, notée f'(x), nous donne des informations cruciales sur son sens de variation. Voici la règle fondamentale:

  • Si f'(x) > 0 sur un intervalle I, alors f est strictement croissante sur I.
  • Si f'(x) < 0 sur un intervalle I, alors f est strictement décroissante sur I.
  • Si f'(x) = 0 sur un intervalle I, alors f est constante sur I.
En résumé, le signe de la dérivée nous indique si la fonction monte (positive), descend (négative) ou reste stable (nulle). C'est un outil puissant pour l'analyse!

Comment construire le tableau de variation

Le tableau de variation est un outil indispensable pour résumer le comportement d'une fonction. Voici les étapes pour le construire:

  1. Calculer la dérivée: Déterminez f'(x).
  2. Trouver les points critiques: Résolvez l'équation f'(x) = 0. Les solutions sont les points critiques de la fonction. Ce sont les points où la tangente à la courbe est horizontale.
  3. Étudier le signe de la dérivée: Déterminez le signe de f'(x) sur les intervalles délimités par les points critiques. Vous pouvez choisir une valeur de test dans chaque intervalle et évaluer f'(x) en ce point.
  4. Construire le tableau: Le tableau aura une ligne pour x, une ligne pour f'(x) et une ligne pour f(x). Remplissez le tableau avec les points critiques, le signe de f'(x) et les flèches indiquant le sens de variation de f(x) (flèche montante pour croissante, flèche descendante pour décroissante).

Exemple 1: Étude de la fonction f(x) = x2 - 4x + 3

  1. Dérivée: f'(x) = 2x - 4
  2. Points critiques: f'(x) = 0 => 2x - 4 = 0 => x = 2
  3. Signe de la dérivée:
    • Pour x < 2, f'(x) < 0 (par exemple, f'(0) = -4)
    • Pour x > 2, f'(x) > 0 (par exemple, f'(3) = 2)
  4. Tableau de variation:
    x-∞2+∞
    f'(x)-0+
    f(x)↘-1 (minimum)↗
La fonction est décroissante sur ]-∞, 2] et croissante sur [2, +∞[. Elle admet un minimum en x=2 de valeur f(2) = -1.

Définition des Extrema

Un extremum d'une fonction est un point où la fonction atteint une valeur maximale ou minimale. On distingue deux types d'extrema:

  • Maximum local: Un point x0 est un maximum local si f(x0) est la plus grande valeur de f(x) dans un voisinage de x0.
  • Minimum local: Un point x0 est un minimum local si f(x0) est la plus petite valeur de f(x) dans un voisinage de x0.
  • Maximum global (ou absolu): Un point x0 est un maximum global si f(x0) est la plus grande valeur de f(x) sur tout son domaine de définition.
  • Minimum global (ou absolu): Un point x0 est un minimum global si f(x0) est la plus petite valeur de f(x) sur tout son domaine de définition.

Identification des Extrema à partir du tableau de variation

Les extrema se trouvent aux points critiques (où f'(x) = 0) ou aux bornes de l'intervalle d'étude. Le tableau de variation nous indique si un point critique est un maximum, un minimum, ou ni l'un ni l'autre:

  • Si f'(x) change de signe de positif à négatif en x0, alors f(x0) est un maximum local.
  • Si f'(x) change de signe de négatif à positif en x0, alors f(x0) est un minimum local.
Pour trouver les extrema globaux, il faut comparer les valeurs de la fonction aux extrema locaux et aux bornes de l'intervalle.

Exemple 2: Détermination des extrema de f(x) = x3 - 3x sur [-2, 2]

  1. Dérivée: f'(x) = 3x2 - 3
  2. Points critiques: f'(x) = 0 => 3x2 - 3 = 0 => x2 = 1 => x = -1 ou x = 1
  3. Signe de la dérivée:
    • Pour x < -1, f'(x) > 0
    • Pour -1 < x < 1, f'(x) < 0
    • Pour x > 1, f'(x) > 0
  4. Tableau de variation:
    x-2-112
    f'(x)+0-0+
    f(x)↘2 (Maximum local)↗-2 (Minimum local)↘
  • Maximum local: f(-1) = 2
  • Minimum local: f(1) = -2
  • Evaluation aux bornes: f(-2) = -2 et f(2) = 2
Donc, le maximum global est 2 (atteint en -1 et 2) et le minimum global est -2 (atteint en -2 et 1).

Ce qu'il faut retenir

  • Le signe de la dérivée f'(x) indique le sens de variation de f(x): positive → croissante, négative → décroissante, nulle → constante.
  • Les points critiques (f'(x) = 0) sont des candidats pour les extrema locaux.
  • Un tableau de variation est un outil puissant pour visualiser le comportement d'une fonction.
  • Les extrema globaux se trouvent parmi les extrema locaux et les valeurs aux bornes de l'intervalle.

← Applications des fonctions quadratiques : Résolution de problèmes →

FAQ

  • Comment savoir si un point critique est un maximum ou un minimum sans tableau de variation?

    Vous pouvez utiliser le test de la dérivée seconde. Si f'(x0) = 0 et f''(x0) > 0, alors f(x0) est un minimum local. Si f'(x0) = 0 et f''(x0) < 0, alors f(x0) est un maximum local.
  • Est-ce qu'une fonction peut avoir plusieurs maximums locaux?

    Oui, une fonction peut avoir plusieurs maximums et minimums locaux. Seuls les maximums et minimums globaux sont uniques (sur un intervalle donné).