Mathématiques > Calcul Matriciel (Terminale - Spécialité) > Matrices > Opérations sur les matrices (addition, soustraction, multiplication par un scalaire)

Opérations Fondamentales sur les Matrices

Découvrez comment additionner, soustraire et multiplier des matrices par un scalaire. Comprenez les conditions de compatibilité et les propriétés de ces opérations.

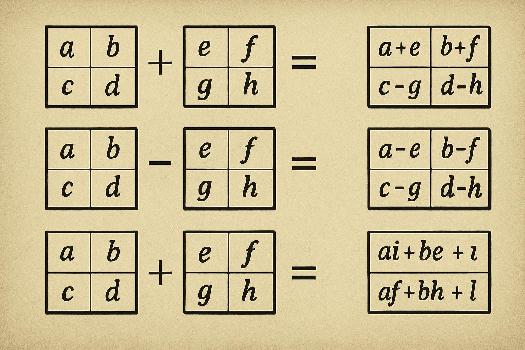
Introduction aux Opérations Matricielles

Les matrices ne sont pas que des tableaux de nombres; elles sont des objets mathématiques qui peuvent être manipulés à travers diverses opérations. Les plus fondamentales sont l'addition, la soustraction et la multiplication par un scalaire. Ces opérations sont essentielles pour comprendre des concepts plus avancés en algèbre linéaire et dans ses applications.

Addition de Matrices

L'addition de matrices est l'une des opérations les plus simples. Pour additionner deux matrices, elles doivent avoir la même dimension (même nombre de lignes et de colonnes). Si A et B sont deux matrices de dimension m x n, alors leur somme, notée A + B, est une matrice C de dimension m x n où chaque élément cij est la somme des éléments correspondants aij et bij.

Formellement: C = A + B où cij = aij + bij.

Exemple:
Soient A =

12
34
et B =
56
78


Alors A + B =
1+52+6
3+74+8
=
68
1012


Attention: On ne peut pas additionner une matrice 2x2 avec une matrice 3x2 par exemple.

Soustraction de Matrices

La soustraction de matrices est similaire à l'addition. Comme pour l'addition, les matrices doivent avoir la même dimension. Si A et B sont deux matrices m x n, alors leur différence, notée A - B, est une matrice C de dimension m x n où chaque élément cij est la différence des éléments correspondants aij et bij.

Formellement: C = A - B où cij = aij - bij.

Exemple:
Soient A =

12
34
et B =
56
78


Alors A - B =
1-52-6
3-74-8
=
-4-4
-4-4

Multiplication d'une Matrice par un Scalaire

La multiplication d'une matrice par un scalaire consiste à multiplier chaque élément de la matrice par ce scalaire. Si A est une matrice de dimension m x n et k est un scalaire (un nombre réel), alors la matrice résultante kA est une matrice de dimension m x n où chaque élément est le produit de k et de l'élément correspondant de A.

Formellement: B = kA où bij = k * aij.

Exemple:
Soit A =

12
34
et k = 2.

Alors 2A =
2*12*2
2*32*4
=
24
68

Propriétés des Opérations

Ces opérations possèdent des propriétés importantes:

  • Commutativité de l'addition: A + B = B + A
  • Associativité de l'addition: (A + B) + C = A + (B + C)
  • Distributivité de la multiplication scalaire: k(A + B) = kA + kB et (k + l)A = kA + lA, où k et l sont des scalaires.

Ce qu'il faut retenir

  • Addition et Soustraction: Les matrices doivent avoir la même dimension pour être additionnées ou soustraites. L'opération se fait élément par élément.
  • Multiplication scalaire: Chaque élément de la matrice est multiplié par le scalaire.
  • Propriétés: L'addition est commutative et associative. La multiplication scalaire est distributive.

← Inverse d'une matrice carrée : Définitions, méthodes et exemples Produit matriciel : Comprendre et maîtriser le calcul matriciel →

FAQ

  • Peut-on additionner une matrice 2x3 et une matrice 3x2 ?

    Non, on ne peut pas. Pour que l'addition soit possible, les matrices doivent avoir exactement la même dimension.
  • Si je multiplie une matrice 3x3 par le scalaire 0, quel est le résultat ?

    Le résultat est une matrice 3x3 dont tous les éléments sont égaux à 0. C'est la matrice nulle.